– дисциплина: (модуль) экономические методы и модели. вуз: фэм cпбгти(ту). тестирование он-лайн. промежуточный тест 3
Выполненные работы
Тестирование он-лайн
Модуль по Экономическим методам и моделям тестирование онлайн, ответы на тесты по (модуль) Экономическим методам и моделям на заказ.
Выполняем тестирование он-лайн для студентов ФЭМ Технологического института по (модуль) Экономическим методам и моделям.
Стоимость прохождения он-лайн тестов за весь курс уточняйте при заказе (присылаете логин и пароль от личного кабинета, мы сообщим Вам стоимость).
Экономические методы и модели (модуль)
ЭММ. Лекция 1. Введение
ЭММ. Лекция 2. Формы записи задачи линейного программирования
ЭММ. Лекция 3. Построение области допустимых планов
ЭММ. Лекция 4. Симплекс-метод решения задачи линейного программирования
ЭММ. Лекция 5. Решение задачи в общем виде. Симплексная таблица
ЭММ. Лекция 6. Метод искусственного базиса
ЭММ. Лекция 7. Двойственность в линейном программировании
ЭММ. Лекция 8. Теоремы двойственности
ЭММ. Лекция 9. Решение задач ЛП с помощью Поиск решения
ЭММ. Лекция 10. Задачи параметрического ЛП
ЭММ. Лекция 11. Графический способ решения
ЭММ. Лекция 12. Алгоритм двойственного симплекс-метода
ЭММ. Лекция 13. Задача параметрического ЛП с парметром в целевой функции
ЭММ. Лекция 14. Постановка транспортной задачи
ЭММ. Лекция 15. Опорный план транспортной задачи
ЭММ. Лекция 16. Метод ветвей и границ. Общая схема
ЭММ. Лекция 17. Постановка задачи о коммивояжере
ЭММ. Лекция 18. Основные понятия теории игр
ЭММ. Лекция 19. Решение матричных игр
ЭММ. Лекция 20. Элементы теории принятия решений
ЭММ. Лекция 21. Спецификация модели
ЭММ. Лекция 22. Коэффициент корреляции
ЭММ. Лекция 23. Линейное уравнение множественной регрессии
ЭММ. Лекция 24. МНК
ЭММ. Лекция 25. Применение МНК
ЭММ. Лекция 26. Методы проверки и исключения
ЭММ. Лекция 27. Современные методы проведения экспертизы
ЭММ. Лекция 28. Подбор экспертов
ЭММ. Лекция 29. Проведение опроса
ЭММ. Лекция 30. Обработка результатов опроса
ЭММ. Лекция 31. Обобщение ранговых оценок
ЭММ. Лекция 32. Оценка согласованности мнений экспертов
ЭММ. Лекция 33. Согласованность ранговых оценок
ЭММ. Лекция 34. Сценарный метод
ЭММ. Лекция 35. Информационные технологии в решении экон задач
ЭММ. Лекция 36. Основные требования информационной безопасности
Промежуточный тест 3
В платежной матрице все элементы положительны. Игра решается в смешанных стратегиях с помощью задачи линейного программирования. Оптимум ЗЛП равен 0,1. Чему равна цена игры?
Ответ
В стандартизованном уравнении регрессии свободный член равен:
Ответ
Для нахождения параметров линейной регрессии минимизируют сумму квадратов отклонений фактических значений результата от подсчитанных по уравнению регрессии. Метод, в основе которого лежит эта идея, – метод … (напишите два слова в родительном падеже):
Ответ
Если дисперсия регрессионных остатков существенно различается, то имеет место … остатков. (напишите существительное в родительном падеже):
Ответ
Исследуется зависимость потребления кофе от его марки, дохода потребителя и цены на кофе. Какой показатель потребует ввести фиктивную переменную?
Ответ
К методам устранения мультиколлинеарности факторных переменных относятся:
1. изменение спецификации модели
2. добавление фиктивных переменных
3. исключение переменных
4. метод наименьших квадратов
Какой критерий позволяет задать меру пессимизма исследователя с помощью специального параметра?
1. критерий Гурвица
2. критерий Сэвиджа (минимаксный риск)
3. критерий Вальда (максиминный выигрыш)
Коэффициент парной корреляции характеризует:
1. тесноту линейной связи между двумя переменными
2. тесноту линейной связи между несколькими переменными
3. тесноту нелинейной связи между двумя переменными
4. тесноту нелинейной связи между несколькими переменными
Матрица рисков имеет вид
3 8 1 0
1 0 2 6
0 2 0 7
Введите номер стратегии, которую надо выбрать по критерию Сэвиджа:
Ответ
На рисунке представлена иллюстрация метода ветвей и границ решения задачи о коммивояжере в виде дерева. Сколько вершин (множеств) рассматривается на иллюстрации?
Ответ
На рынке могут возникнуть десять вариантов различных ситуаций. Чему равна вероятность определенной ситуации, если используется критерий Лапласа?
Ответ
На рынке могут возникнуть три варианта условий с вероятностями соответственно 0,3, 0,3 и 0,4. При выпуске определенного вида продукции фирма может получить в этих условиях прибыль соответственно 100, 200 и 100 ден. ед. Чему равна ожидаемая прибыль?
Ответ
Платежная матрица имеет вид:
7 11 6
4 5 8
8 10 4
Верхняя цена игры равна:
Ответ
Примерами фиктивных переменных могут служить:
1. Образование
2. Пол
3. Возраст
4. Доход
Разделив коэффициент ковариации на произведение стандартных отклонений переменных, получают коэффициент … (напишите существительное в родительном падеже):
Ответ
Спецификация эконометрической модели двухфакторной регрессии предполагает, что число всех переменных (зависимой и независимых) равно:
Ответ
Среднее произведение отклонений значений переменных от своих средних – коэффициент… (напишите существительное в родительном падеже):
Ответ
Что такое бесконечная игра?
1. игра, в которой хотя бы у одного игрока имеется бесконечное число стратегий
2. игра, которая повторяется бесконечное число раз
3. игра, в которой у каждого игрока имеется бесконечное число стратегий
Что такое оптимальная стратегия?
1. та, которая в каждой отдельно взятой игре обеспечивает данному игроку максимально возможный выигрыш (или минимальный проигрыш)
2. та, которая при многократном повторении игры обеспечивает данному игроку максимально возможный средний выигрыш (или минимальный средний проигрыш)
3. та, которая при многократном повторении игры обеспечивает данному игроку максимально возможную дисперсию выигрыша
Эффективной оценкой называется та, у которой:
1. смещенность выше
2. дисперсия минимальна
3. отсутствует смещенность
4. дисперсия максимальна
Для заказа он-лайн тестирования по экономическим методам и моделям присылайте свой логин и пароль.
Лекция 01
,
Лекция 02
,
Лекция 03
,
Лекция 04
,
Лекция 05
,
Лекция 06
,
Лекция 07
,
Лекция 08
,
Лекция 09
,
Лекция 10
,
Лекция 11
,
Лекция 12
,
Лекция 13
,
Лекция 14
,
Лекция 15
,
Лекция 16
,
Лекция 17
,
Лекция 18
,
Лекция 19
,
Лекция 20
,
Лекция 21
,
Лекция 22
,
Лекция 23
,
Лекция 24
,
Лекция 25
,
Лекция 26
,
Лекция 27
,
Лекция 28
,
Лекция 29
,
Лекция 30
,
Лекция 31
,
Лекция 32
,
Лекция 33
,
Лекция 34
,
Лекция 35
,
Лекция 36
,
Промежуточный тест 1
,
Промежуточный тест 2
,
Промежуточный тест 3
,
ЭММ. Итоговый тест
6 Бюджетное ограничение и полезность | Экономика для школьников
Бюджетное ограничение
показывает все наборы товаров, доступные потребителю при данном уровне дохода.
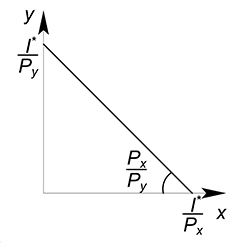
Рассмотрим случай, когда товаров всего 2:
$I=P_xcdot{x} P_ycdot{y}$
В данной формуле I обозначает доход; $P_x$, $P_y$ – цены товаров; $x$, $y$ – их количества.
 Определение 2
Определение 2
Пусть потребитель (как обычно) потребляет два товара – x и y. тогда назовем U(x, y) такое число, что чем потребителю лучше от потребления x и y, тем оно больше. если в каких-то двух наборах U совпадает, то для потребителя эти наборы эквивалентны.
Функция полезности показывает зависимость между количеством потребленного товара и полученной от потребления полезностью.
Определение 3
Кривая безразличия показывает все товарные наборы, приносящие потребителю одинаковый уровень полезности.
Пример 1
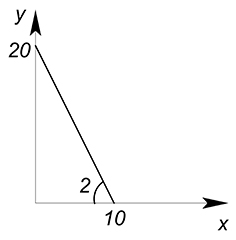
Цена товара $x$ равна 10 д.ед., цена товара $y$ составляет 5 д.ед. Доход равен 100 д.ед. Функция полезности задана уравнением $U=xy$. Найти оптимальное количество потребления двух благ.
В задачах на данную тему нам необходимо выбрать оптимальную комбинацию потребления товаров, которая будет приносить максимально возможный уровень полезности при заданном уровне дохода. Метод, используемый в задачах данного типа, похож на метод максимизации выручки
Построим график функции бюджетного ограничения.
$100=10x 5y$
$y=20-2x$
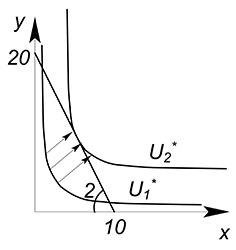
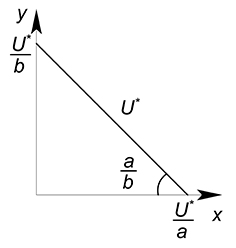
Функция полезности задана уравнением $U=xy$. Зафиксируем переменную $U$ на некотором уровне $U^*$, получим функцию, зависящую от одной переменной $x$:
$y=dfrac{U^*}{x}$
Изобразив на одном графике бюджетное ограничение и функцию полезности, начнем двигать функцию полезности вверх, пока она не достигнет максимально высокого уровня, то есть, пока прямая бюджетного ограничения не станет касательной к графику функции полезности.
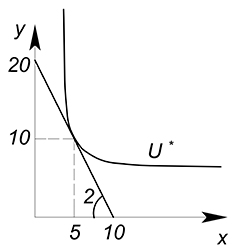
Теперь приравняем производную функции бюджетного ограничения ($y'(x)=-2$) к производной кривой безразличия ($y'(x)=-dfrac{U^*}{x^2}$).
$-2=-dfrac{U^*}{x^2}$
$x^2={U^*}{2}$
$x=sqrt{dfrac{U^*}{2}}$ (выбираем, естественно, положительный корень)
$y=sqrt{2U^*}$
Мы получили оптимальные объёмы товаров $x$ и $y$ при данной функции полезности и соотношении цен товаров. Теперь найдем их числовое значение, помня про размер нашего дохода (найдем точку на прямой бюджетного ограничения, дающую максимальный уровень полезности):
$I=10sqrt{dfrac{U^*}{2}} 5sqrt{2U^*}=100$
Решим данное уравнение, получим максимально возможное значение полезности при данном уровне дохода:
$U^*=50$
Найдем соответствующую ему оптимальную комбинацию $x$ и $y$:
$x=5$
$y=10$
Здесь это можно также решить гораздо проще, если выразить $y$ из бюджетного ограничения и подставить в функцию полезности. Сразу же получится квадратичная парабола.
$U=x(f(x))$, где $f(x)$ – функция бюджетного ограничения.
Пример 2
Если у нас абсолютно взаимозаменяемые (для потребителя не имеет значения иметь единицу $x$ или единицу $y$, если на рынке один из товаров стоит дороже, то потребитель не будет его покупать) товары заменяются друг на друга в постоянной пропорции, вне зависимости от количества благ.
$U=ax by$
Пропорция всегда постоянна – функция полезности линейна при зафиксированном уровне $U^*$.
Цена товара $x$ равна 10 д.ед., цена товара $y$ составляет 5 д.ед. Доход равен 100 д.ед. Функция полезности задана уравнением $U=x y$. Найти оптимальное количество потребления двух благ.
Аналогично с задачей 1 построим график функции бюджетного ограничения.
$100=10x 5y$
$y=20-2x$

Дальше будем поступать аналогично случаю, когда КПВ у нас линейная (это ведь тоже бюджетное ограничение), и мы ищем максимально доступную выручку (сейчас максимальный уровень полезности).
Зафиксируем $U^*$, выразим $y$ через $x$:
$y=U^*-x$
Начнем двигать вверх данную прямую, пока она не достигнет максимально высокого положения из вcех возможных.
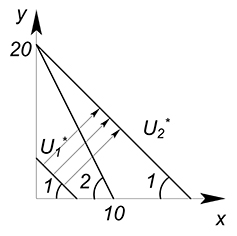
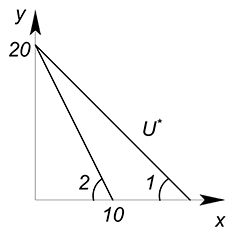
Получим оптимальную точку $x=0$, $y=20$, $U=20$.
 Пример 3
Пример 3
Если товары являются взамодополняющими, функция полезности будет иметь вид:
$U=min(ax;by)$
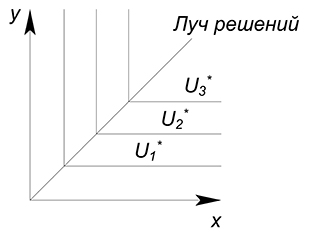
Если товары потребуются только в комплекте, то дополнительная единица одного из благ не принесет увеличения уровня полезности. Увеличение объёма только одного блага бессмысленно, ибо получить больший уровень полезности можно только при пропорциональном увеличении количества обоих благ.
В данном случае решение будет лежать на луче решений, который будет проходить через вершины углов кривых безразличия.
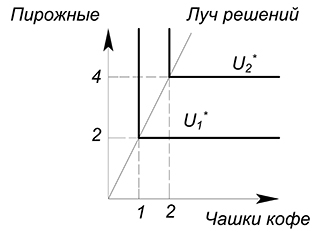
Цена товара $x$ равна 10 д.ед., цена товара $y$ составляет 5 д.ед. Доход равен 100 д.ед. Функция полезности задана уравнением $U=min(x;y)$. Найти оптимальное количество потребления двух благ.
$100=10x 5y$
$y=20-2x$

Функция полезности. Пропорция $x:y$ равна $1:1$, луч решений будет иметь вид
$y=x$
Нарисуем все на одном графике. Будем двигаться вверх вдоль луча решений до точки его пересечения с графиком бюджетного ограничения:
Найдем оптимальные объёмы товаров:
$y=x=dfrac{20}{3}$
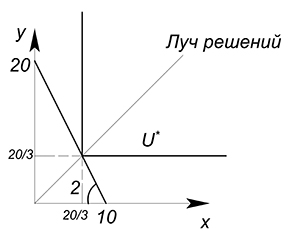
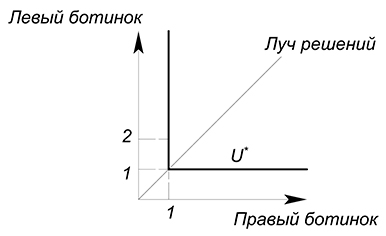
Выше мы рассмотрели случай с пропорцией потребления $1:1$. Такая пропорция подходит, например, для такого товара как ботинки. Если у нас будет 2 левых и 1 правый ботинок, то такая комбинация принесет такой же уровень полезности, как комплект из 1 правого и 1 левого ботинка (если нам доступна комбинация $2 1$, то мы не перейдем на более высокую кривую безразличия, а просто продвинемся вдоль одной из осей старой):
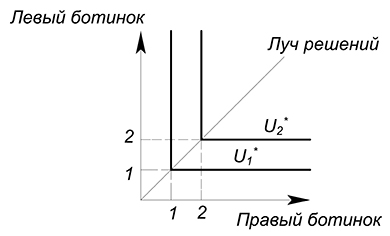
А комплект с пропорциональным увеличением обоих благ уже будет обладать большей полезностью:
Но вообще пропорции потребления могут быть любыми. Решение тогда все равно будет лежать на луче, проходящем через вершины углов кривых безразличия. Например, можно всегда потреблять комплект 1 чашка кофе 2 пирожных. Тогда при увеличении количества чашек кофе, нужно пропорционально увеличивать количество пирожных. Если мы купим 1 чашку кофе и 3 пирожных, мы получим тот же уровень полезности, что и когда мы приобретали 1 кофе и 2 пирожных:
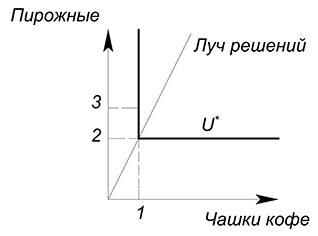
Луч решений будет задаваться функцией $y=2x$, если по оси $x$ отложены чашки кофе, а по оси $y$ – пирожные.
§
§
Спрос (D – demand)
– зависимость между ценой и количеством экономического блага, которое потребители
хотят
и
готовы (финансово могут)
приобрести в течение некоторого промежутка времени. Может описываться функциями $Q(P)$ или $P(Q)$.
Возможный вид кривой спроса:
 Определение 2
Определение 2
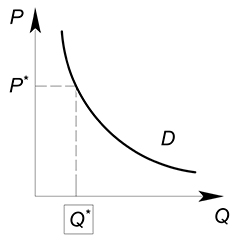
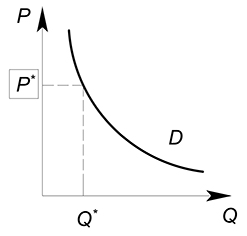
Величина спроса – максимальное количество экономического блага, которое потребители желают и готовы купить при данном значении цены.
 Определение 3
Определение 3
Цена спроса – максимальное значение цены, при котором потребители желают и готовы купить данное количество экономического блага.
Существует закономерность, актуальная для многих товаров, но не для всех. Эта закономерность называется законом спроса.
Закон спроса: при повышении цены экономического блага величина спроса сокращается, то есть имеет место отрицательная зависимость между ценой товара и величиной спроса. Следовательно, график спроса зачастую имеет отрицательный наклон.
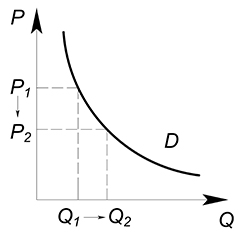
При изменении величины спроса сама функция спроса не изменяется. Мы просто переходим из одной точки графика спроса в другую, двигаемся вдоль кривой спроса. Причиной изменения величины спроса является изменение цены данного блага.
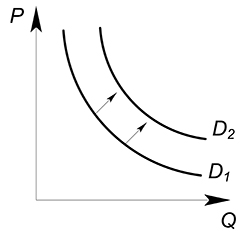
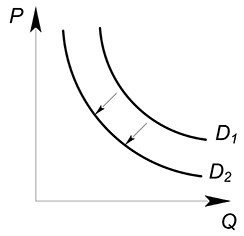
При изменении спроса меняется вся функциональная зависимость. Изменяется количество потребляемого блага при каждом возможном уровне цены.
График спроса двигается либо вправо вверх (при увеличении спроса),
либо влево вниз (при уменьшении спроса).
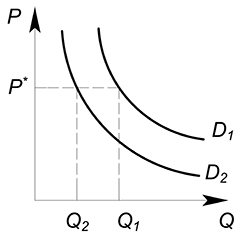
Увеличение спроса означает, что при данном уровне цены покупатель теперь хочет и может купить большее количество блага, чем раньше ($Q_2>Q_1$):
уменьшение спроса означает, соответственно, что теперь покупатель хочет и может купить меньшее количество блага при данной цене ($Q_2 < Q_1$):
Возможные причины изменения спроса:
- Изменение цены заменяющего товара.
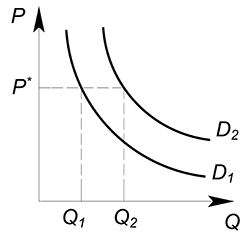
Пусть у нас имеется 2 товара-заменителя $x$ и $y$ (для нас не имеет значения, какой товар потреблять). Если цена товара $y$ понизится, то величина спроса на данный товар увеличится. Мы перейдем из точки $Q_1$ в точку $Q_2$. Так как теперь нам более выгодно покупать товар $y$. Следовательно, при каждом возможном значении цены товара $x$ количество покупаемого блага $x$ может уменьшиться. Спрос на товар $x$ уменьшается.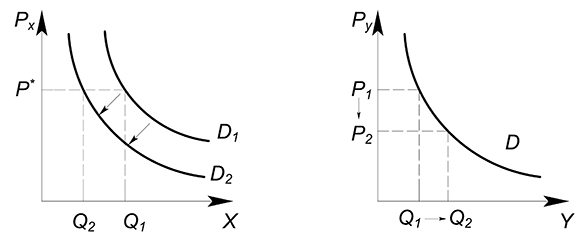
- Изменение цены дополняющего блага.
Также пусть имеется 2 блага $x$ и $y$, только теперь они употребляются в определенной пропорции. Предположим, что цена товара $y$ уменьшилась. Теперь мы можем тратить меньше денег на покупку старого количества данного блага. Сэкономленные деньги можно пустить на приобретение дополнительных комплектов обоих товаров. Следовательно, при каждом возможном значении цены товара $x$ можно потреблять большее количество данного блага. Спрос на товар $x$ увеличивается.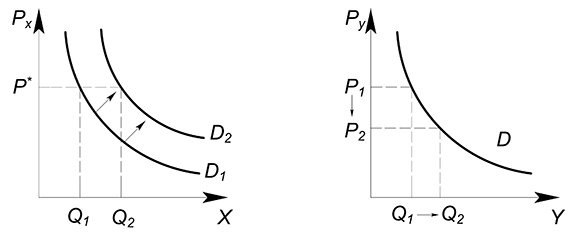
- Доход потребителя.
Здесь следует сказать, что существуют нормальные экономические блага и инфериорные.Определение 4
Нормальное экономическое благо – такой товар, спрос на который растет с увеличением дохода потребителя.Определение 5
Инфериорное экономическое благо такой товар, спрос на который уменьшается с увеличением дохода потребителя. - Количество покупателей.
При увеличении количества покупателей спрос увеличивается, при уменьшении, соответсвенно, уменьшается. - Вкусы, мода, сезонность…
В моду могут войти, например, желтые галстуки, тогда спрос на них вырастет. Зимой, например, может увеличится спрос на лыжи, а летом – на велосипеды.
§
На рынке зачастую существует большое количество покупателей, имеющих различные функции спроса. В некоторых задачах нужно найти
рыночный спрос
– количество товара, покупаемого всеми потребителями при каждом уровне цены.
Существует великое разнообразие функций спроса. Разберемся с сложением типичных функций на данных примерах:
Задача 1
Пусть спрос первой группы потребителей описывается функцией $Q=10-P$; второй группы $Q=15-3P$. Найти рыночный спрос.
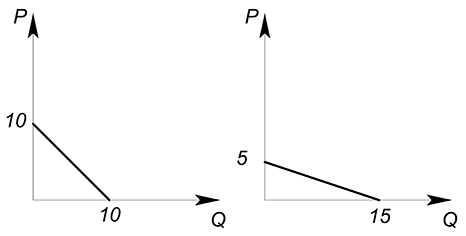
Первый покупатель вступает на рынок при цене, равной 10, второй – при цене, равной 5. Следовательно, спрос на данном участке, при $P$ принадлежащей промежутку $[10;5)$, предъявляется только первой группой покупателей: $Q=10-P$. Две группы потребителей покупают данный товар при $P$, принадлежащей промежутку $[5;0]$. Для получения функции рыночного спроса мы имеем право сложить функции спроса двух групп: $Q=10-P 15-3P=25-4P$.
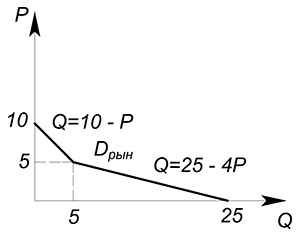
Ответ: $Q=10-P$, если $P in [10;5)$; $P=25-4P$, $P in [5;0]$.
Задача 2
Сложите данные функции спроса:
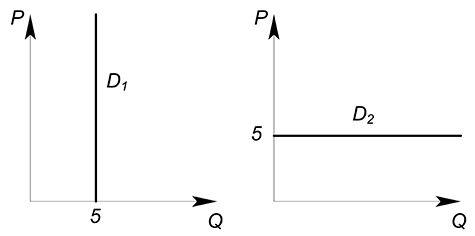
Первая группа потребителей будет покупать максимально 5 единиц товара при любой цене, а вторая группа готова приобретать любое количество товара при цене не большей 5.
При $P=infty$ покупается 5 единиц товара. Следующий потребитель вступает при цене, равной 5. При данной цене будет покупаться $Q=infty$.
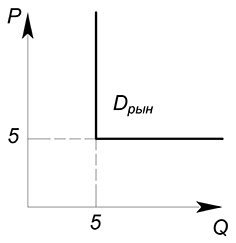
§
Экономическим агентом, производящим различные товары и услуги, является фирма. На рынке именно фирмы формируют предложение экономических благ. О фирме и её деятельности мы будем говорить несколько следующих недель.
Основной целью деятельности фирмы является максимизация прибыли (прибыль часто обозначается символом $pi$). Что такое прибыль? Это разница между выручкой ($TR$, как мы помним) и общими издержками ($TC$ – total cost) – то количество денег, которое фирма заработала, минус то количество денег, которое она потратила.
$pi=TR-TC$
Функция прибыли является зависимостью между количеством экономического блага, которое фирма может произвести, и, собственно, самой прибылью, которую она получит от продажи некоторого объёма блага:
$pi(Q)=TR(Q)-TC(Q)$
Перед тем как перейти к максимизации прибыли остановимся поподробнее на теме выручки и теме издержек.
§
Выручка (TR)
– это доход (денежная сумма), который фирма получает от продажи по некоторой цене какого-то количества произведенной продукции:
$TR=Pcdot Q$
Функция выручки – зависимость между количеством производимого блага и величиной денежной суммы, получаемой от продажи товара. Функция выручки выводится из спроса:
$TR=P(Q)cdot Q$
Функции выручки могут иметь совершенно разнообразный вид:
Пример 1
Функция спроса описывается зависимостью $Q(P)=dfrac{100}{P}$. Найти функцию выручки.
Выразим обратную функцию спроса: $P(Q)=dfrac{100}{Q}$; теперь найдем функцию выручки: $TR=dfrac{100}{Q} cdot Q=100$. В данном случае выручка постоянна, не зависит от количества производимого блага и равна 100.
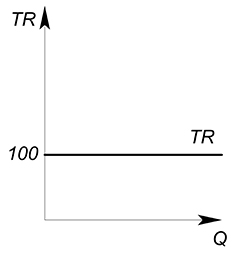
Подробнее о функции выручки мы будем говорить, когда будем изучать рыночные структуры.
Определение 2
Средняя выручка (AR – average revenue) показывает, какую выручку в среднем приносит единица продаваемого товара:
$AR=dfrac{TR}{Q}$
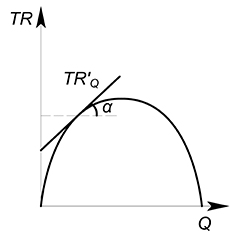
Геометрический смысл средней выручки – тангенс угла наклона луча (секущей), проведенного из начала координат к какой-нибудь точке на графике выручки:
$tg alpha = dfrac {TR^*}{Q^*}$
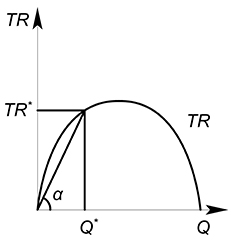
Проведя огромное количество лучей к графику выручки мы сможем получить график средней выручки $AR$.
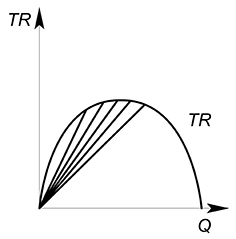
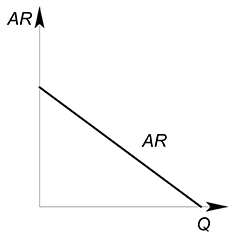
Так среднюю выручку можно описать функцией, вид которой будет совпадать с обратной функцией спроса:
$AR=dfrac{TR(Q)}{Q}=P(Q)$
 Определение 3
Определение 3
Предельная выручка (MR – marginal revenue) показывает, какую выручку принесет дополнительная произведенная единица товара.
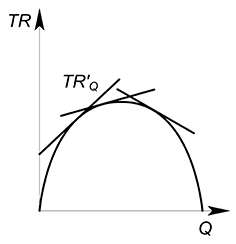
В дискретном случае предельная выручка будет равна $MR=dfrac {TR_2-TR_1}{Q_2-Q_1}=dfrac{Delta TR}{Delta Q}$
Геометрический смысл предельной выручки – тангенс угла наклона секущей, соединяющей точки $(Q_2;TR_2)$ и $(Q_1;TR_1)$.
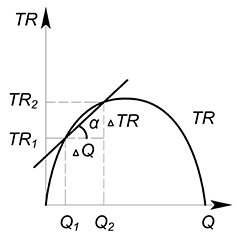
Если мы предполагаем, что производимый нами товар является бесконечно делимым, то нам будет интересно узнать какую выручку принесет дополнительная бесконечно малая единица выпускаемого блага.
Тогда геометрический смысл в данном случае будет следующий: MR есть тангенс угла наклона касательной, проведенной к графику функции выручки в интересующей нас точке.
Проведя множество касательных к разным точкам сможем построить функцию предельной выручки:
В данном случае предельная выручка будет производной функции выручки: $MR(Q)=TR'(Q)$.
Пример 2
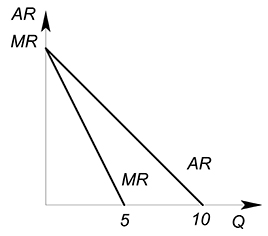
Функция спроса описывается уравнением $Q(P)=10-P$. Найти функции TR, AR, MR и изобразить их графики.
Выразим обратную функцию спроса: $P(Q)=10-Q$. Теперь найдем функцию выручки: $TR(Q)=P(Q)cdot Q=10Q-Q^2$. Можно найти функции средней и предельной выручки: $AR(Q)=dfrac {TR(Q)}{Q}=10-Q$, $MR(Q)=TR'(Q)=10-2Q$. Изобразим графики:
 Максимизация функции выручки выполняется так же, как и любой другой функции – можно использовать производную (подробнее о максимизации функции можете узнать здесь), а можно обойтись без нее (подробнее здесь)
Максимизация функции выручки выполняется так же, как и любой другой функции – можно использовать производную (подробнее о максимизации функции можете узнать здесь), а можно обойтись без нее (подробнее здесь)
Пример 3
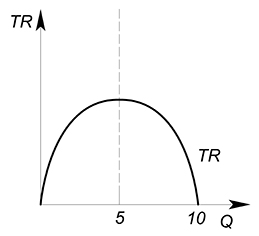
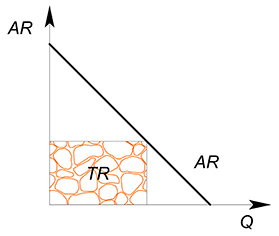
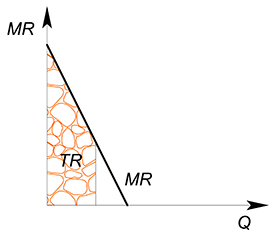
Обратная функция спроса имеет вид: $P(Q)=20-2Q$. Найти максимальную выручку.
Запишем функцию выручки: $TR=20Q-2Q^2$. Это парабола, ветви вниз. Найдем точку максимума: $x_0=-dfrac{b}{2a}=dfrac{20}{4}=5$. Подставим данную точку в функцию выручки: $TR=20cdot 5-2cdot 25=100-50=50$.
Также для функции $AR$ $TR$ в точке будет является произведением значений координат на осях:
для $MR$ – $TR$ в точке есть площадь под графиком функции, слева ограниченная осью $P$, справа перпендикуляром к оси $Q$, проведенным из интересующей нас точки:
§
Фирмы являются основными поставщиками продукции на рынки. Для производства экономических благ фирмы привлекают необходимые ресурсы и поэтому несут некоторые издержки.
Общие издержки (TC – total cost) – затраты, связанные с использованием всех ресурсов, задействованных в производстве блага.
Издержки могут быть явными и неявными. Явные издержки – это затраты на привлечение различных факторов производства (ресурсов). К явным издержкам могут относиться, например, зарплата работников или затраты на аренду помещения. Неявные издержки – это альтернативная стоимость собственных средств, то есть наша упущенная выгода – стоимость наилучшего из всех вариантов вложения собственных ресурсов, от которого мы отказались ради использования их в данном деле. Например, если некто мог бы получать в трех разных местах зарплату в 60, 70, 80 тысяч долларов в месяц, то альтернативная стоимость руководства собственным предприятием для него равна 80 тысяч долларов в месяц. Это его неявные издержки.
$TC{экономические}=TC{явные} TC{неявные}$
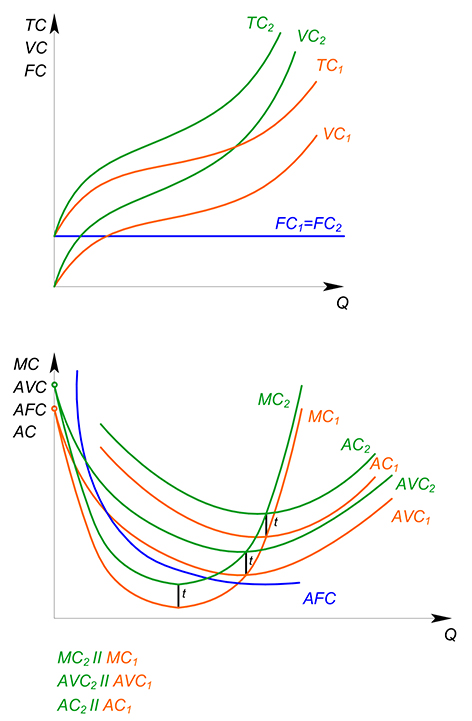
Как уже было сказано выше, фирма для производства продукции привлекает определенные ресурсы – использует различные факторы производства. В задачах мы будем говорить об использовании только двух факторов производства – труда (L) и капитала (K). Ответ на вопрос “что такое труд?” довольно очевиден, а что же такое капитал? Это все оборудование, которое используется в процессе производства – станки, здания, сооружения… Мы будем рассматривать в задачах только издержки, связанные с использованием труда и с использованием капитала. Также мы будем разделять издержки на переменные (VC – variable cost) и постоянные издержки (FC – fixed cost).
Группа, к которой относятся издержки зависит от периода, в котором работает фирма.
Переменные издержки – затраты, связанные с использованием переменного фактора производства. Переменный фактор производства – такой ресурс, количество которого мы можем изменить в данном периоде.
Постоянные издержки связаны с использованием ресурса, количество которого мы не можем изменить в данном периоде.
Всего выделяют три периода:
Долгосрочный период (LR – long run) – период, в котором все факторы производства – и труд, и капитал – являются переменными. Это относительно большой промежуток времени, за который можно изменить и количество труда, и количество капитала – нанять или уволить рабочих, закупить и установить новые станки, построить новое здание для завода.
$TC=VC$
$VC=w cdot L r cdot K$, где w (wages) – зарплата работникам, L – их количество, r (rate) – плата за капитал, K – количество капитала.
Краткосрочный период (SR – short run) – период, в котором один из факторов производства является переменным, другой – постоянным – затраты на труд являются переменными издержками, а на капитал – постоянными. Это время, за которое можно нанять новых работников, например, но нельзя заменить оборудование.
$TC=VC FC$
$VC=wcdot L$
$FC=rcdot K$
Мгновенный период – все ресурсы являются постоянными.
$TC=FC$
$FC=w cdot L r cdot K$
Общие издержки могут задаваться функцией, зависящей от количества производимой продукции, ибо для производства разных объемов товара может быть целесообразно использование разного количества ресурсов. Функция издержек является неубывающей функцией (предположите, почему).
$TC(Q)=VC(Q)$ – в LR – можно изменять количество и переменного, и постоянного фактора производства
$TC(Q)=VC(Q) FC$ – в SR – изменять можно только количество переменного фактора производства
Поговорим более подробно о краткосрочном периоде.
$TC=VC(Q) FC$
$VC(Q)=wcdot L$ – переменные издержки – затраты на труд.
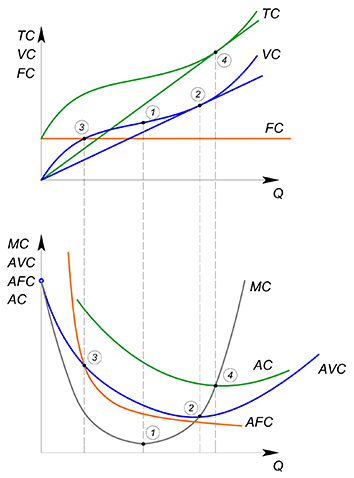
$AVC(Q) =dfrac{VC(Q)}{Q}$ – средние переменные издержки. Показывают, какое количество переменного фактора производства (труда) необходимо для производства единицы продукции.
Геометрический смысл средних переменных издержек такой же как и у средней выручки – тангенс угла наклона луча, проведенного из начала координат, к интересующей нас точке.
$FC=const=rcdot K$ – постоянные издержки. Показывают затраты, которые мы несем при использовании имеющегося у нас количества постоянного фактора производства (капитала).
Имея функцию общих издержек постоянные затраты можно посчитать так: подставляем $Q=0$, получаем $TC(0)=FC$
$AFC(Q)=dfrac{FC}{Q}$ – средние постоянные издержки. Показывают, какое количество постоянного фактора производства (капитала) необходимо для производства единицы продукции.
Геометрический смысл средних постоянных издержек – тангенс угла наклона луча, проведенного из начала координат, к интересующей нас точке.
$AC(Q)=dfrac{VC(Q) FC}{Q}=AVC(Q) AFC(Q)$ – средние общие издержки. Показывают, какое количество переменного и постоянного факторов производства необходимо для производства единицы продукции.
Геометрический смысл средних общих издержек аналогичен геометрическому смыслу других средних величин.
Предельные издержки (MC – marginal cost) – затраты, которые мы понесем при производстве дополнительной единицы блага.
В дискретном случае $MC=dfrac{MC_2-MC_1}{Q_2-Q_1}$
Геометрический смысл предельных издержек в данном случае – тангенс угла наклона секущей, соединяющей точки $(Q_1;MC_1)$ и $(Q_2;MC_2)$.
Если товар бесконечно делим, то $MC(Q)=TC'(Q)=VC'(Q)$
Геометрический смысл предельных издержек в этой ситуации – тангенс угла наклона касательной, проведенной к графику $TC$ или $VC$ в интересующей нас нас точке
 Пример
Пример
Функция средних переменных издержек имеет вид $AVC(Q)=17$, средних постоянных – $AFC(Q)=dfrac{10}{Q}$. Найдите функцию общих издержек
$AC(Q)=AVC(Q) AFC(Q)=17 dfrac{10}{Q}$
$TC(Q)=AC(Q)cdot Q = 17Q 10$
§
Фирма производит свою продукцию, следуя определенной
технологии
.
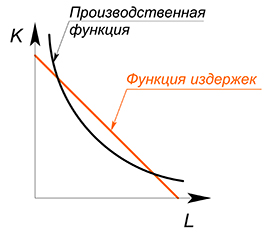
Производственная функция показывает налучшую технологическую зависимость между количеством используемых ресурсов и объемом выпуска.
$Q=f(L;K)$
Из производственной функции можно вывести функцию издержек.
Пример 1
Дано: $Q= L cdot K$, $w=4$, $r=1$, найти функцию общих издержек.
В данном случае можно или минимизировать издержки при выбранном уровне $Q$, или максимизировать объем выпуска при данном уровне издержек.
Воспользуемся методом 2:
$TC=wL rK$
$TC=4L K$
Как уже не раз случалось, мы опять встречаем функцию, зависящую от двух переменных. Зафиксируем $TC$, выразим $L$ через $K$:
$K=TC^*-4L$
Что касается производственной функции – зафиксируем $Q$, выразим $L$ через $K$:
$K=dfrac{Q^*}{L}$
Имеем схожую ситуацию с задачей максимизации полезности, только в данном случае у нас цель – максимизировать объем выпускаемой продукции:
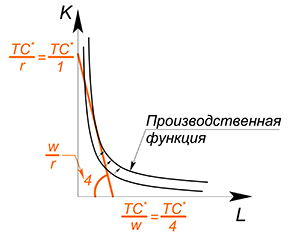
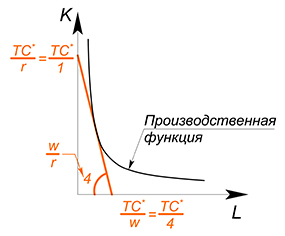
Возьмем производную обеих функций по $L$, найдем точку, в которой они равны, найдем точку касания графиков
(Почему именно касания? Если бы мы выбрали более низкий уровень $Q^*$, то мы получили бы более низкую производственную функцию, произвели бы меньше продукции с теми же издержками:
Если мы бы выбрали слишком высокий уровень $Q$, то данный объем производства был бы недостижим при данном уровне издержек:
$-4=-dfrac{Q^*}{L^2}$
Выразим $L$ ($L>0$):
$L=sqrt{dfrac{Q^*}{4}}=dfrac{sqrt {Q^*}}{2}$
Подставим в производственную функцию, выразим $K$:
$K=2sqrt{Q^*}$
Теперь подставим $L$ и $K$ в функцию издержек, $Q$ снова является переменной:
$TC=dfrac{4sqrt{Q}}{2} 2sqrt{Q}=4sqrt{Q}$
 Пример 2
Пример 2
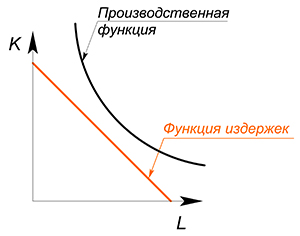
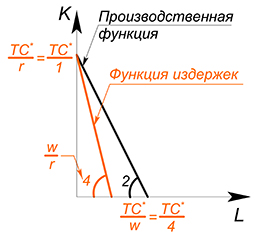
Производственная функция является линейной: $Q=2L K$, $w=4$, $r=1$, $TC(Q)-?$
Действовать будем в целом аналогично предыдущему варианту, но в этот раз попробуем использовать метод 1: будем минимизировать издержки при выбранном уровне $Q$:
$TC=4L K$
$K=TC^*-4L$
$K=Q^*-2L$
Имеем 2 линейные функции, будем двигать функцию издержек вниз, пока она не достигнет оптимального положения:
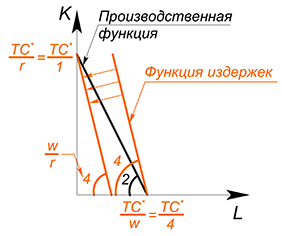
(Если мы выберем более высокий уровень издержек, то вступим нерационально – такой же объем выпуска при больших издержках. Зачем? Если выбрать более низкий уровень издержек, то невозможно будет произвести нужный объем продукции) .
Оптимальное положение будет достигнуто в точке, где количество капитала максимально, а труда равно нулю. Тогда:
$Q=K$
$TC=K$
$TC=Q$
 Эффект масштаба показывает во сколько раз изменится $Q$ после увеличения всех используемых ресурсов в одинаковое число раз $t$ по сравнению с первоначальным $Q$, увеличенным в $t$ раз.
Эффект масштаба показывает во сколько раз изменится $Q$ после увеличения всех используемых ресурсов в одинаковое число раз $t$ по сравнению с первоначальным $Q$, увеличенным в $t$ раз.
$Q_{новое}(tL;tK)$ vs $tQ(L;K)$
Если $Q_{новое}(tL;tK) > tQ(L;K)$, то эффект масштаба положительный, если $Q_{новое}(tL;tK)=tQ(L;K)$, то постоянный, если $Q_{новое}(tL;tK) < tQ(L;K)$, то эффект масштаба отрицательный.
Пример 3
$Q=4L K^2$, какой эффект масштаба наблюдается в данной ситуации?
$(tK)^2 4tL$ vs $t(K^2 4L)$
$t^2K^2 4tL$ vs $tK^2 4tL$
$t^2$ vs $t$
$t>1$, следовательно эффект масштаба положительный
TP – total product (он же Q), общий продукт труда – показывает зависимость объема выпуска продукции от количества переменного ресурса при прочих равных условиях.
Функция $TP$:
i участок – функция растет ускоряющимся темпом, при найме каждого последующего работника объем выпуска увеличивается на все большую и большую величину;
ii участок – функция растет замедляющимся темпом, при найме каждого дополнительного работника объем выпуска увеличивается на все меньшую величину;
iii участок – $TP$ убывает. При производстве товара может наступить такой момент, когда дополнительная единица переменного ресурса (труда обычно) уже не способствует увеличению производимой продукции. Дополнительно нанятый работник может только мешать. Например, если у нас имеется всего один станок, и мы наняли 50 рабочих, то они будут только мешать друг другу, стопившись у этого единственного механизма.
$AP_(L)$ average product, средний продукт (труда) – показывает, сколько в среднем единиц продукции приходится на одну единицу переменного ресурса:
$AP_L=dfrac{TP}{L}$ (бывает $AP_K=dfrac{TP}{K}$)
$AP_L(L)=dfrac{TP(L)}{L}$
Геометрический смысл среднего среднего продукта труда такой же как и у других средних величин – тангенс угла наклона луча, проведенного из начала координат (секущей) к точке на графике общего продукта труда.
$MP_(L)$ – marginal product, предельный продукт (труда) – показывает прирост общего продукта при увеличении переменного ресурса на единицу.
В дискретном случае $MP_L=dfrac{TP_2-TP_1}{L_2-L_1}$.
Геометрический смысл предельного продукта в данном случае – тангенс угла наклона секущей, соединяющей точки $(L_1;TP_1)$ и $(L_2;TP_2)$.
Если ресурс бесконечно делим, то $MP_L=TP'(L)$
Геометрический смысл предельного продукта в этой ситуации – тангенс угла наклона касательной, проведенной к графику $TP$ в интересующей нас нас точке.
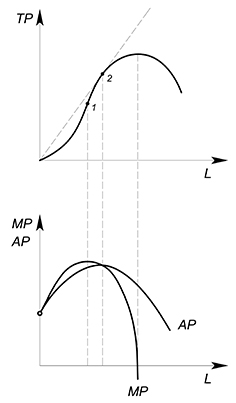 Пример 4
Пример 4
$Q(L)=30L-L^2$, найти $AP_L$, $MP_L$
$AP_L=dfrac{Q(L)}{L}=30-L$
$MP_L=Q'(L)=30-2L$
§
§
На рынке могут складываться специфические условия, оказывающие заметное влияние на деятельность фирм. Главными особенностями совершенно конкурентного рынка являются:
- Большое количество фирм, каждая фирма имеет небольшую долю рынка большое количество покупателей
- Однородность продаваемого товара – для потребителя не имеет значения, какой товар покупать, он не различает продукцию различных фирм
- Отсутствие барьеров входа/выхода – любая фирма способна начать безубыточное функционирование (не надо покупать лицензию, нет необходимости в больших вложениях в оборудование); любая фирма способна прекратить производство без дополнительных издержек, связанных с ликвидацией
- На совершенно конкурентном рынке отсутствует стратегическое поведение фирм. Каждая фирма слишком мала для того, чтобы своими действиями повлиять на остальной объем продаж и цену на рынке. Отдельный продавец, конечно, может установить на свой товар цену, отличную от рыночной, но если его цена будет выше цены, по которой продают его конкуренты, то никто не купит товар данного продавца, а если его цена будет ниже сложившейся на рынке цены, то он, возможно, просто продаст свой товар быстрее остальных производителей, также в данном случае фирма может получить отрицательную прибыль, рыночная цена при этом не поменяется. Также у фирм на совершенно конкурентном рынке нет рыночной власти – фирма не может повлиять на цену, сложившуюся на рынке, путем изменения количества продаваемой продукции. Покупатели также не имеют монопольной власти на совершенно конкурентном рынке – их как и фирм слишком много
- На совершенно конкурентном рынке царствует полная информированность – все продавцы и все покупатели знают все о каждой совершенной сделке, о количестве проданной продукции, о ее цене.
- На рынке данного типа отсутствует неценовая конкуренция – фирмы, например, не рекламируют свой товар. Им это невыгодно, ибо рекламные издержки увеличивают общие затраты фирмы, что для нее не очень благоприятно – если она увеличит цену (а конкуренты оставят ее на прежнем уровне), чтобы покрыть издержки на рекламу, она лишится всех своих покупателей, если она не станет менять цену, то ее прибыль по сравнению со страной уменьшится, ибо фирме не стоит рассчитывать на компенсацию издержек на рекламу за счет большого увеличения количества покупателей – товар на рынке однородный, прирост покупок может равномерно распределиться среди всех продавцов
Совершенная конкуренция в чистом виде в реальности довольно редкое явление. Биржевая торговля кофе или пшеницей может подойти под данное описание.
§
На совершенно конкурентном рынке готовность фирм продать какое-то количество товара по какой-то цене описывается функцией
предложения ($S$ – supply).
Функция предложения ($P(Q)$) показывает, какое количество товара по какой цене фирма готова продать. Рыночная функция предложения, так же как и рыночная функция спроса, получается путем суммирования индивидуальных функций предложения (функций предложения отдельных фирм).
На нерегулируемом рынке продается и покупается такое количество продукции и по такой цене, которые устраивают и продавцов, и покупателей. Равновесная цена ($P^*$) и равновесное количество ($Q^*$) продукции соответствуют точке пересечения кривых спроса и предложения.:
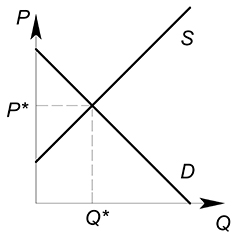
Именно цену в точке равновесия ($P^*$) каждая отдельная фирма воспринимает как заданную.
Обозначим эту цену просто за $P$. $P=const$. Тогда $TR=P cdot Q=const cdot Q$.
Фирма не может повлиять на цену, сложившуюся на рынке, как мы уже говорили в предыдущем уроке. Также ей невыгодно устанавливать на свою продукцию отличную от рыночной цену.
Запишем функцию прибыли некой фирмы на каком-либо совершенно конкурентном рынке:
$pi(Q)=TR(Q) -TC(Q)=P cdot Q-TC(Q)$
Рационально действующая фирма будет максимизировать свою прибыль. Найдем производную функции прибыли и приравняем ее к 0:
$pi'(Q)=TR'(Q)-TC'(Q)=MR(Q)-MC(Q)=P-MC=0$
Отсюда найдем оптимальное количество производства товара, сделаем проверку на $min$/$max$. Выберем точку, где функция прибыли достигает максимального значения.
Например, это может выглядеть так:
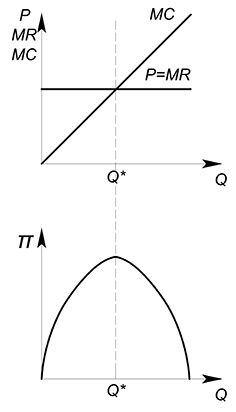
Как мы видим, обычно фирма получает максимальную прибыль в точке, где предельная выручка равна предельным издержкам. Если точка максимума функции всего одна, как в нашем примере, левее этой точки функция прибыли возрастает, такую ситуацию можно улучшить – произвести большее количество продукции и получить большую прибыль; правее этой точки функция убывает, производство каждой последующей единицы продукции будет уменьшать общую прибыль фирмы.
Для максимизации прибыли фирма выбирает для каждого возможного значения $MR$ оптимальное значение $MC$. Так как на совершенно конкурентном рынке значение предельной выручки при каждом значении $Q$ совпадает со значением цены, то функцией предложения отдельной фирмы принято считать часть ее функции предельных издержек. Для каждого значения цены фирма выберет свое оптимальное количество производимого товара, следуя правилу $MR=MC$, где в данном случае $MR=P$.
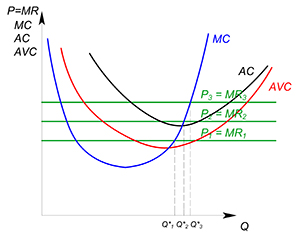
Но индивидуальной функцией предложения фирмы будет не вся ее функция предельных издержек, а только возрастающий фрагмент, лежащий выше значения функции средних переменных издержек в точке минимума.
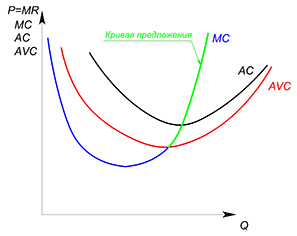
Почему именно так?
Мы выбираем возрастающий участок, ибо в точке пересечения $MR$ и $MC$ на убывающем участке функции предельных издержек функция прибыли достигает своего минимального значения – величина переменных издержек в этой точке (площадь под графиком $MC$) больше, чем величина выручки (площадь под графиком $MR$).
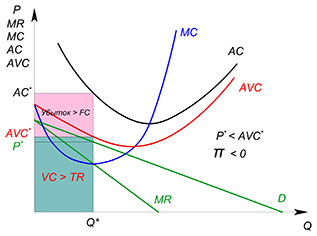
Фирма может работать рынке или покинуть его, если ее не будет удовлетворять получаемая прибыль. В краткосрочном периоде фирма может уйти в убыток, размер которого способен достигать значения постоянных издержек. Фирма будет оставаться на рынке до тех пор, пока получаемая выручка будет покрывать переменные издержки (пока цена продукции не будет ниже минимального значения функции средних переменных издержек; если цена опустится ниже, фирма уйдет с рынка и уже не будет предлагать продукцию):
Фирма остается, если:
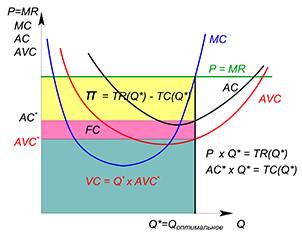
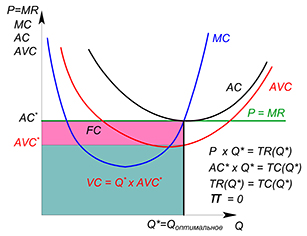
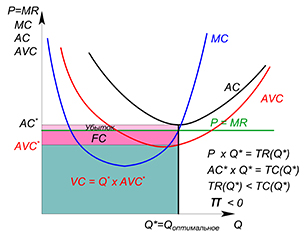
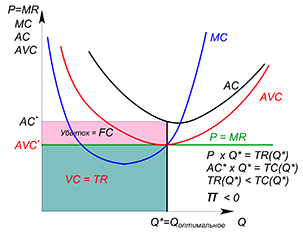
Фирма уходит, если:

В долгосрочном периоде считается, что фирмы, получающие какие-нибудь убытки будут постепенно уходить из отрасли, рыночное предложение за счет этого будет уменьшаться, кривая рыночного предложения сдвинется влево вверх. Таким образом, равновесия цена подимется, убытки фирм, оставшихся на рынке уменьшатся. Рынок придет в равновесие. Фирмы будут получать нулевую экономическую прибыль ($pi{экономическая}=TR-TC{экономические}$). У фирм, находящихся на рынке будут отсутствовать стимулы покидать отрасль, у фирм, потенциально способных войти на рынок, исчезнут стимулы это делать (если бы экономическая прибыль была бы положительной, этот рынок был бы сверхприбыльным, у новых фирм были бы стимулы работать на нем).
Если фирмы получают нулевую экономическую прибыль, их выручка равна экономическим издержкам, следовательно, цена равна минимуму средних общих издержек.
Пример 1
На совершенно конкурентном рынке товара установилась цена, равная 16, функция издержек фирмы имеет вид $TC(Q)=Q^2 5$, найти максимальную прибыль фирмы.
$pi=16Q-Q^2-5$
$pi'(Q)=16-2Q=0$
$Q^*=8$
$pi=128-64-5=59$, $pi>0$, фирма остется на рынке
Пример 2
На совершенно конкурентном рынке присутствуют 100 фирм, имеющих одинаковые функции издержек: $TC(Q)=Q^2 5$; спрос задан функцией $Q=100-P$, найти рыночную функцию предложения, равновесную цену и равновесное количество, если обратная функция спроса имеет вид $P=100-0{,}98Q$
Выведем индивидуальную функцию предложения каждой фирмы:
$MC(Q)=TC'(Q)=2Q$
$AVC(Q)=Q$
$AVC$ достигает своего минимального значения в точке $Q=0$, дальше $MC$ проходит всегда выше $AVC$, следовательно, в данном случае кривой предложения одной фирмы будет весь график $MC$.
Найдем рыночное предложение:
$MC=2Q$
$Q=dfrac{MC}{2}$
$Q{рын}=dfrac{100MC}{2}=50MC$
$MC=dfrac{Q}{50}$
$P=dfrac{Q}{50}$ $Q$ принадлежит $[-infty; infty]$
$dfrac{Q}{50}=100-0{,}98Q$
$Q=5000-49Q$
$50Q=5000$
$Q^*=100$
$P^*=dfrac{100}{50}=100-0{,}98 cdot 100 =2$
§
§
- Товар на рынке производит одна фирма, покупателей же большое количество
- Предлагаемый товар уникален, не имеет близких заменителей
- Барьеры входа/выхода на рынок очень высокие (патенты, наличие на рынке государственной монополии…)
- На данном рынке отсутствуют стратегическое поведение фирм и неценовая конкуренция, ибо на нем работает всего лишь одна фирма, обладающая монопольной властью. Покупатели же такой властью не обладают.
- Информированность на данном рынке неполная – на нем присутствует асимметрия информации
Монополия и максимизация прибыли
Для фирмы-монополиста рыночный спрос на производимый ею товар совпадает со спросом на продукцию данной фирмы.
На рынке, где царствует монополист, не существует кривой предложения производимого товара.
Фирма максимизирует свою функцию прибыли ($pi=P{рын}(Q)cdot Q – TC(Q)$), находит оптимальный объем выпуска $Q^*$, затем, исходя из готовности покупателей платить, выбирает оптимальную цену на свою продукцию.
Пример 1
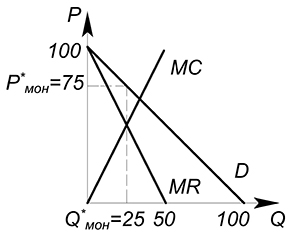
Спрос на продукцию монополиста задан функцией $Q(P)=100-P$, издержки данной фирмы описываются уравнением $TC(Q)=Q^2$, найти оптимальные объем выпуска и цену.
$P(Q)=100-Q$
$pi (Q)=TR(Q)-TC(Q)=(100-Q)Q-Q^2=100Q-2Q^2$
$pi'(Q)=MR(Q)-MC(Q)=100-4Q=0$
$Q^*=25$
$P^*=P(Q^*)=100-25=75$
 Монополия и совершенная конкуренция
Монополия и совершенная конкуренция
Сравним ситуацию, когда фирма ведет себя как монополист, со случаем, когда фирму заставили вести себя как совершенно конкурентную.
Пример 2
Возьмем данные из предыдущей задачи. Оптимальные цену и количество монополиста мы уже знаем – они равны 75 д.ед и 25 шт. Чтобы найти совершенно конкурентное равновесие выведем функцию предложения фирмы:
$MC=2Q$, $ACV$ в данном случае всегда меньше или равно $MC$
Следовательно, $P=2Q$
Мы нашли обратную функцию предложения фирмы, которая будет одновременно и обратной функцией рыночного предложения, ибо фирма всего одна. Приравняем полученную функцию к обратной функции спроса:
$100-Q=2Q$
$3Q=100$
$Q^*=33dfrac{1}{3}$
$P^*=66dfrac{2}{3}$
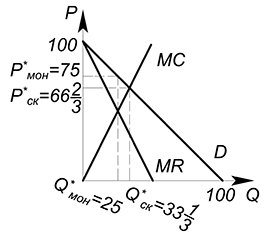
Как мы видим, в случае, когда фирма ведет себя как совершенный конкурент, количество производимого товара больше, а цена продажи меньше. Бо’льшую прибыль фирма получает при монополии, ибо тогда она, максимизируя функцию прибыли, выбирает именно ту точку, которая принесет ей максимальную прибыль ($Q{мон}$). $Q{ск}$ обычно не совпадает с монопольным объемом производства продукции, следовательно, производство $Q{ск}$ приносит меньшую прибыль, чем производство $Q{мон}$.
Как бы хороша ни была участь монополиста, иногда и такой фирме приходится покинуть рынок:
В отличие от совершенно конкурентной фирмы монополия может получать и в краткосрочном и долгосрочном периодах как отрицательную, так и положительную экономическую прибыль.
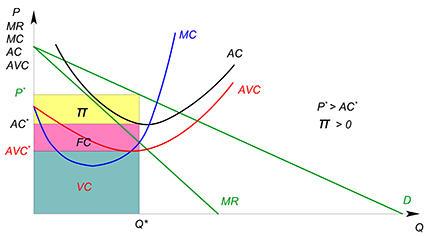
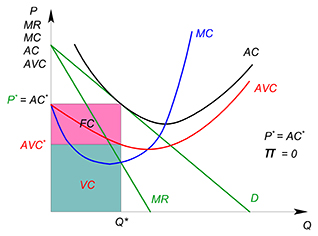
Фирма остается в обоих периодах:
В данных ситуациях у фирмы существуют стимулы покинуть рынок в долгосрочном периоде. Она сделает это, если затраты на преодоление барьеров выхода окажутся меньше, чем получаемые фирмой убытки:

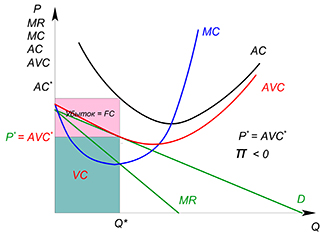
Фирма уходит:
 Индекс Лернера:
Индекс Лернера:
Может пригодиться при решении задач
$dfrac{P-MC}{P}$
§
§
§
§
На рынке труда со стороны
предложения
труда ($L_S$) выступают работники.
Рыночное предложение труда выглядит так:
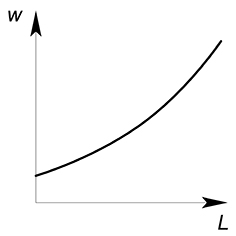
При увеличении величины ставки заработной платы количество работников, готовых трудиться, увеличивается.
Фирмы же предъявляют спрос на труд ($L_D$). Основной целью рационально действующй фирмы является максимизация прибыли. Прибыль фирмы зависит от объема произведенной продукции ($pi(Q)$), который в свою очередь зависит от количества используемого для его изготовления фактора производства, в данном случае труда ($Q(L)$). Таким образом, функция прибыли фирмы может быть выражена через $L$.
$pi(L)=TR(L)-TC(L)$
Такую функцию прибыли можно максимизировать по $L$.
$pi'(L)=TR'(L)-TC'(L)=MRP_L-MC_L=0$
После взятия производной, ее приравнивания к нулю и дальнейшей проверки мы найдем, какое количество труда фирме выгодно будет нанять для максимизации своей прибыли
$MRP_L$ – это предельный доход труда в денежном выражении. Показывает доход, полученный фирмой при найме дополнительного работника.
$MC_L$ – предельные издержки труда, затраты фирмы на найм дополнительного работника.
На рынке труда могут встречаться совершенно различные рыночные структуры.
Сравним совершенно конкурентный рынок труда с монополизированным, где работает профсоюз (действия профсоюза эквивалентны действиям монополиста).
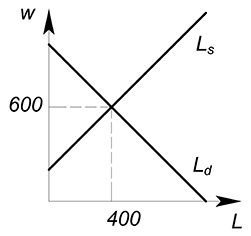
$L_D=1000-w$, $MC_L=-200 w$ (В ск $L_S$), найти оптимальное количество нанимаемого труда на совершенно конкурентном рынке данного фактора производства и на монополизированном.
Совершенная конкуренция:
Равновесие на совершенно конкурентном рынке труда достигается также как и на совершенно конкурентном товарном рынке – в точке пересечения кривой спроса с кривой предложения.
$1000-w=-200 w$
$w_{ск}=600$
$L_{ск}=400$
 Профсоюз:
Профсоюз:
Спрос на труд предъявляют фирмы, максимизирующие свою прибыль, профсоюз, выступающий со стороны продавцов, также максимизирует свою прибыль.
$L_D=1000-w$
$w=1000-L_D$
$TR(L)=w(L)cdot L=1000L-L^2$
$MRP_L=TR'(L)=1000-2L$
$MRP_L=MC_L$
$1000-2L=L 200$
$L=dfrac{800}{3}$
Выполним проверку:
$pi'(L)=MRP_L-MC_L=800-3L$
$pi”(L)=-3$
$-3 < 0$, следовательно в точке экстремума находится максимум функции.
Таким образом:
$L_{мон}=dfrac{800}{3}$
Подставляем полученное значение в функцию спроса на труд:
$w_{мон}=dfrac{2200}{3}$
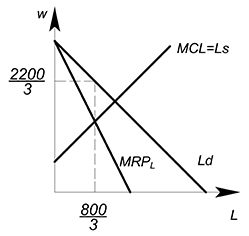
Естественно, у профсоюза как у монополиста нет функции предложения. На графике надпись “$MC_L=L_S$” обозначает, какую кривую надо брать за $MC_L$
$w_{ск} < w_{мон}$
$L_{ск} > L_{мон}$
§
§
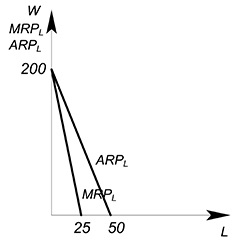
Так как фирма работает на совершенно конкурентном рынке труда, то она воспринимает ставку заработной платы, сложившуюся на рынке, как заданную, $w=const$. Функция предложения труда для одной фирмы представляет собой прямую линию, параллельную оси абсцисс, проходящую на уровне равновесной рыночной ставки заработной платы, $w^*=MC_L$.
Фирма выбирает оптимальный для себя объем труда, исходя из стремления максимизировать прибыль. Кривой спроса фирмы на труд является нисходящая ветвь $MRP_L$ (не работаем на восходящем участке, ибо там максимум убытков) ниже наибольшего значения $ARP_L$ (в $SR$ фирма работает, если $TRge VC$, поедим обе части уравнения на $L$, получим $ARP_Lge w$)
Пример
Некоторая фирма является монополистом на рынке товара. Функция спроса на ее товар имеет вид $Q=100-P$. Технология изготовления данного товара описывается функцией $Q=2L$. Вывести функцию спроса фирмы на труд.
$P(Q)=100-Q$
$pi(Q)=100Q-Q^2-TC(Q)$
$TC(Q)=VC(Q) FC$
Так $w=const$, ибо рынок труда совершенно конкурентный, то $VC=wcdot L$
Таким образом, получаем:
$pi(L)=200L-4L^2-wL-FC$
Фирма максимизирует прибыль, при каждом возможном уровне ставки заработной платы она будет нанимать оптимальное число рабочих, соответствующих условию максимизации прибыли:
$pi'(L)=200-8L-w=0$
$pi”(L)=-8<0$, следовательно, максимум.
Делаем еще одну проверку (уходит ли фирма или остается):
$TR(L)=200L-4L^2$
$ARP_L=200-4L$, всегда выше функции $w=200-8L$
Получаем функцию спроса фирмы на труд:
$L=25-0{,}125w$
$Max pi$ в зависимости от рынка товара и ресурса:
Общие условия: $MR(L)cdot MP_L = w'(L) w (L)$ (берем производную сложной функции: $VC(L)=w(L)cdot L$, $VC'(L)=w'(L) w(L)$ -по правилу дифференцирования суммы. Аналогично поступаем с $TR$.
- Если товарный рынок совершенно конкурентный, рынок труда нет, то $Pcdot MP_L = w'(L) w(L)$
- Если ресурсный рынок совершенно конкурентный, то $MR cdot MP_L=w$
- Если оба рынка совершенно конкурентные, то $Pcdot MP_L =w$
Всегда не забываем делать проверку, остается ли фирма на рынке! ($MRP_L le ARP_L$)
§
§
Государство может ограничивать объемы продаж на рынке. Посмотрим, что будет происходить на различных рынках при введении квот.
Обозначим за $Q_{max}$ – такой объем продаж, который будет максимально возможным из всех разрешенных государством; за $Q^*$ – равновесный объем продаж на рынке до введения квоты.
Совершенно конкурентный рынок:
Если $Q_{max}ge Q^*$, то на рынке, естественно, будет продаваться такое количество товара, которое продавалось в равновесии до введения квоты.
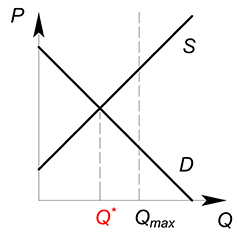
Если же $Q_{max}< Q^*$, на рынке будет продаваться максимально близкое (из разрешенных) к оптимальному $Q^*$ количество товара – $Q_{max}$.
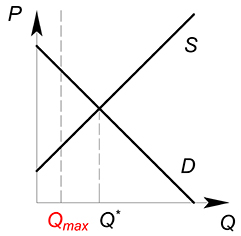 Монополия:
Монополия:
Как и на совершенно конкурентном рынке, если $Q_{max}ge Q^*$, то будет продаваться некоторое количество товара, которое было оптимальным до введения ограничений.
Если $Q_{max} < Q^*$, монополия будет производить $Q_{max}$ объем продукции, как наиболее близкий к оптимальному.
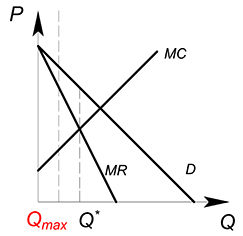
При введении квоты фирмы могут начать получать убытки, так что необходимо проверять, останутся ли они на рынке или уйдут.
§
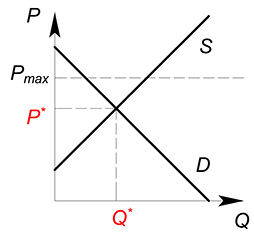
Государство может установить максимально возможную цену на какую-либо продукцию, фирмы не имеют права продавать данный товар по цене выше установленного потолка.
Пусть $P_{max}$ – потолок цены, $P^*$ – равновесная цена, сложившаяся на рынке до вмешательства государства
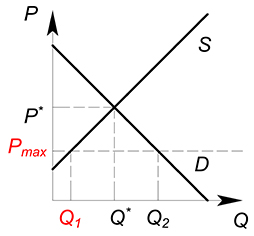
Совершенная конкуренция
Если $P_{max}ge P^*$, очевидно, что на рынке будет продаваться то равновесное количество блага по той равновесной цене, которые сложились до государственного вмешательства.
В случае $P_{max} < P^*$, цена продаж будет равняться $P_{max}$ (фирмы захотят продать свой товар по той цене, которая будет наиболее близко к оптимальной), при этой цене мы видим, что покупатели готовы приобрести $Q_2$ единиц продукции, что больше, чем готовы продать производители ($Q_1$), фактически же будет продан меньший из рассматриваемых объемов – $Q_1$.
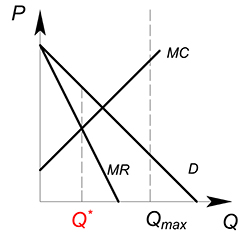
 Монополия
Монополия
Аналогично совершенно конкурентному рынку, если $P_{max}ge P^*$, на монополизированном рынке будет продаваться тот объем продукции, который был оптимальным до введения потолка цен, по старой оптимальной цене.
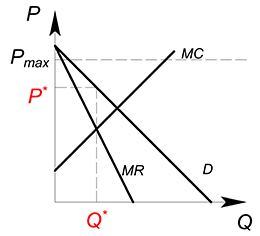
Если $P_{max} < P^*$, то монополист будет продавать свою продукцию по $P_{max}$.
Установим $P_{max}$ на уровне старой оптимальной цены, будем пускать данную прямую до точки пересечения $D$ с $MC$. Монополия будет выпускать при данных значениях $P_{max}$ такой объем товара, которы будет соответствовать точке пересечения прямых $D$ и $P_{max}$.
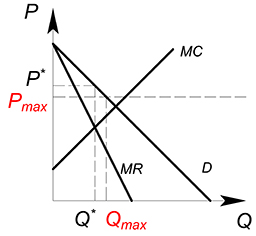
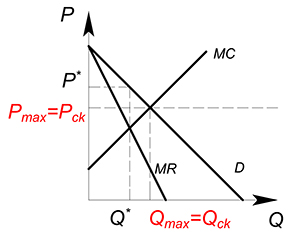
Когда $P_{max}=D=MC$ на рынке будет продаваться совершенно конкурентный объем блага по совершенно конкурентной цене.
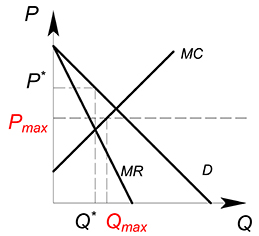
Начнем опускать линию $P_{max}$ ниже точки пересечения спроса и предельных издержек. Теперь фирма будет производить то количество продукции, которое будет соответствовать точке пересечения $MC$ и $P_{max}$
 Пол цены
Пол цены
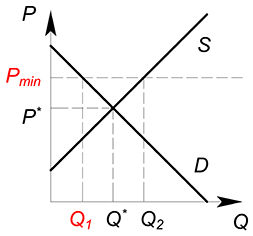
Государство устанавливает минимально возможную цену, по которой можно продавать продукцию (обозначим ее за $P_{min}$, $P^*$ – равновесия цена, установившаяся на рынке до вмешательства государства).
Совершенная конкуренция
Если $P_{min} le P^*$, на рынке, естественно, будет продаваться тот объем продукции, который был равновесным и до вмешательства государства, цена на данный товар также будет прежняя.
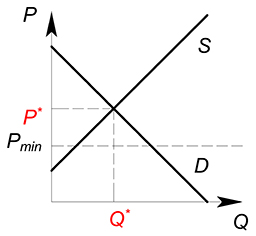
Если $P_{min} > P^*$, цена продаж будет составлять $P_{min}$, при данной цене производители будут готовы продать $Q_2$ единиц продукции, а покупатели будут согласны купить $Q_1$ единиц продукции, $Q_1 < Q_2$, фактический объем продаж на рынке будет $Q_1$, меньший из рассмотренных.
 Монополия
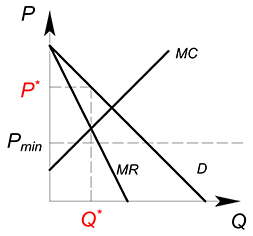
Монополия
Аналогично с совершенной конкуренцией, если $P_{min}le P^*$, монополия будет продавать свой старый оптимальный объем продукции по старой оптимальной цене.
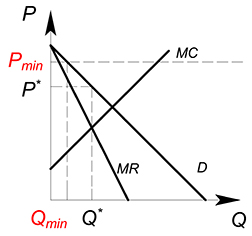
Если же $P_{min} > P^*$, то монополия будет продавать тот объем товара, который будет соответствовать пересечению кривых $D$ и $P_{min}$.
Не забываем проверять, останутся ли фирмы на рынке после вмешательства государства!
§
— особый вид налога, сумма которого не зависит от количества товара, производимого фирмой. В краткосрочном периоде данный налог относится к квазипостоянным издержкам фирмы.
$TC(Q)=VC(Q) FC T$, где $T$ – величина фиксированного аккордного налога, не зависящая от $Q$, в точке, где $Q=0$, $T$ также равен 0, при других объемах выпуска $T$ это число.
Фирма может уйти с рынка в краткосрочном периоде. Допустим, что $TR-VC=50$, $FC=100$, $T=500$, при положительном выпуске, 0 при нулевом. Если фирма уйдет с рынка, она понесет издержки, равные постоянным (100), если решит остаться, то заплатит налог, прибыль будет равна $-550$, дешевле уйти. Фирма уходит с рынка, если прибыль от производства нулевого объема товара больше, чем от производства оптимального ( оптимального в условиях отсутствия налога).
Влияние аккордного налога на издержки фирмы: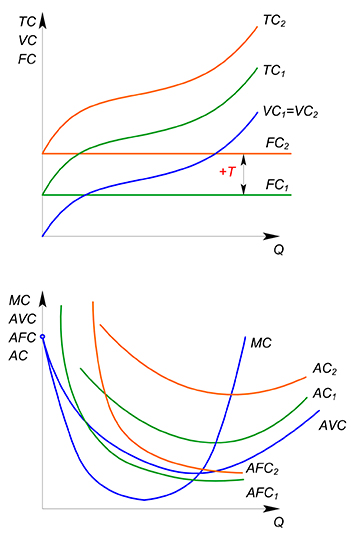 Пример
Пример
На рынке действует монополист, спрос на его продукцию описывается обратной функцией $P=100-Q$, издержки имеют вид $TC(Q)=Q^2 100$. На фирму был введен аккордный налог, равный $400$ д.ед. Найдите прибыль фирмы после введения налога.
Запишем функцию прибыли фирмы после введения налога:
$pi(Q) = (100-Q)Q-Q^2-100-400=100Q-2Q^2-500$
Максимизируем прибыль фирмы:
$pi'(Q)=100-4Q=0$
$Q^*=25$
$pi”(Q)=-4<0$, следовательно, максимум
Подставим найденное оптимальное $Q$ в функцию прибыли:
$pi(25)=750>0$, фирма остается на рынке
Аккордная субсидия
Введение аккордной субсидии обратно введению аккордного налога. Если при фиксированном налоге прибыль фирмы уменьшалась на величину, равную величине налога, то при субсидировании прибыль фирмы увеличится на величину введенной субсидии.
§
– налог, представляющий собой фиксированную сумму, взимаемую с единицы продукции.
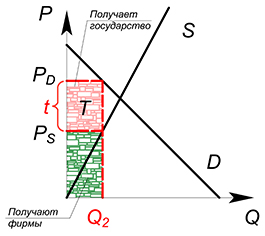
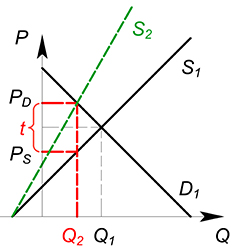
Рассмотрим некий рынок (возьмем для примера совершенно конкурентный). Раньше, до вмешательства государства, на данном рынке продавалось некоторое количество продукции $Q^*$ по цене $P^*$. Сумму, которую потребители уплачивали за единицу продукции, полностью получали производители. Цена покупки $P_D$ была равна цене продажи $P_S$.
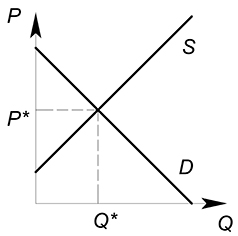
Представим, что государство ввело на данном рынке потоварный налог по ставке $t$. Теперь фирма должна, получив от покупателя сумму $P_D$ за единицу продукции, отдать государству часть этой суммы, равную ставке налога $t$. В новых условиях фирма получает сумму $P_D-t$ за единицу товара. Фактически для фирмы уменьшилась цена, по которой она продает свой продукт. $P_S=P_D-t$. При введении налога количество покупаемого и продаваемого товара уменьшается.
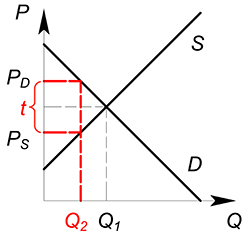
Действие, которое оказывает налог на ситуацию на рынке, эквивалентно снижению спроса или увеличению издержек. Налог, наложенный на покупателя, окажет такое же влияние на рынок, что и налог, наложенный на производителя.
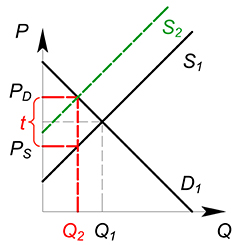
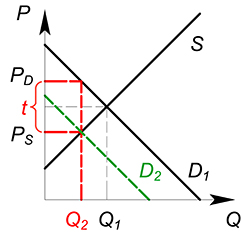 Рассмотрим, какое действие оказывает налог на функции издержек одной фирмы:
Рассмотрим, какое действие оказывает налог на функции издержек одной фирмы:
$TC(Q)_2=TC(Q)_1 tQ$
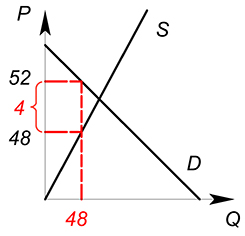
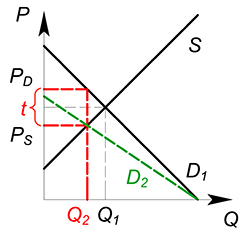
 Пример 1
Пример 1
Спрос на совершенно конкурентном рынке задан функцией $Q_D=100-P_D$, предложение – $Q_S=P_S$, государство вводит налог по ставке 4, найти равновесное количество продаваемого товара, цену покупателя ($P_D$), цену продавца ($P_S$).
Решать такую задачу удобно, составив следующую систему уравнений:
$begin {cases}
Q_D=100-P_D\
Q_S=P_S\
Q_D=Q_S\
P_D=P_S 4
end {cases}$
Отсюда получаем:
$100-(P_S 4)=P_S$
$P_S=48$
$P_D=48 4=52$
$Q_D=Q_S=48$
 Пример 2
Пример 2
Спрос на совершенно конкурентном рынке задан функцией $Q_D=100-P_D$, предложение – $Q_S=P_S$, государство хочет максимизировать сумму налоговых поступлений. Найдите $Q^*$, $P_D$, $P_S$, оптимальную ставку налога, сумму налоговых поступлений, построить кривую Лаффера
$begin {cases}
Q_D=100-P_D\
Q_S=P_S\
Q_D=Q_S\
P_D=P_S t
end {cases}$
$100-P_S-t=P_S$
$P_S=dfrac{100-t}{2}$
$Q_S=P_S=dfrac{100-t}{2}$
Сумма налоговых поступлений будет равна ставке налога, умноженной на количество проданного товара:
$T=tcdot Q^*$
$T(t)=tcdot Q(t)$
$T(t)=tcdot (dfrac{100-t}{2})=50t-0{,}5t^2$
Данная функция, описывающая зависимость суммы налоговых поступлений от ставки налога, называется кривой Лаффера.
Максимизируем данную функцию:
$T'(t)=50-t$
$t^*=50$
$T”(t)=-1<0$, максимум
Теперь изобразим ее:
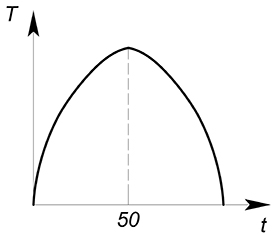
$Q_D=Q_S=25$
$P_D=75$
$P_S=25$
$T=50cdot 25=1250$
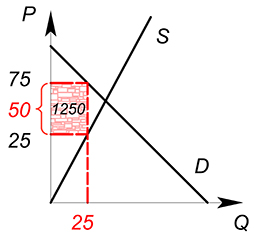 Пример 3
Пример 3
Принцип введения налога на монополизированном рынке такой же как и на совершенно конкурентном.
$P_D(Q)=100-Q$, $TC(Q)=Q^2 10$, $t=510$, найти прибыль фирмы после введения налога
Введем налог на продавца. Он увеличивает издержки фирмы:
$TC(Q)_2=TC(Q)_1 tQ=Q^2 10Q 10$
$pi(Q)=100Q-Q^2-Q^2-10Q-10=90Q-2Q^2-10$
$pi'(Q)=90-4Q=0$
$Q^*=22{,}5$
$pi(Q)=1002{,}5>0$, фирма остается на рынке
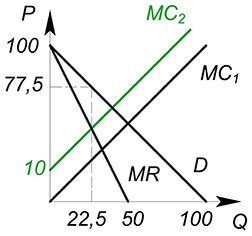 Пример 4
Пример 4
Действие потоварной субсидии обратно действию потоварного налога.
Спрос на совершенно конкурентном рынке задан функцией $Q_D=100-P_D$, предложение – $Q_S=P_S$, государство вводит субсидию по ставке 4, найти равновесное количество продаваемого товара, цену покупателя ($P_D$), цену продавца ($P_S$).
Покупатель платит за единицу товара $P_D$ меньшую $P_S=P_D s$
$begin {cases}
Q_D=100-P_D\
Q_S=P_S\
Q_D=Q_S\
P_D=P_S-4
end {cases}$
$100-P_S s=P_S$
$P_S=52$
$P_D=48$
$Q_S=Q_D=52$
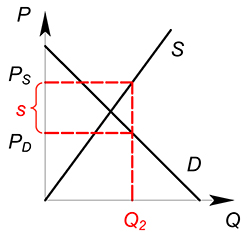
§
налог, взимаемый в процентах от цены продаваемого товара.
Налог может считаться в процентах от цены потребителя (в долях), тогда $P_S=(1-t)cdot P_D$, или же от цены производителя $P_D=(1 t)cdot P_S$.
Данный налог, наложенный на потребителя, влияет на рынок также как и налог, наложенный на производителя. Аналогично потоварному налогу стоимостной налог “уменьшает” спрос или увеличивает издержки производителей:
 Пример 1
Пример 1
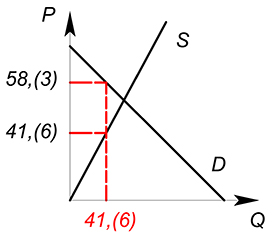
На совершенно конкурентном рынке функция спроса на товар имеет вид $Q_D=100-P_D$, предложения – $Q_S=P_S$, государство вводит стоимостной налог – 40% от цены производителя. Найти $P_D$, $P_S$, $Q^*$ после введения налога.
$P_D=(1 0{,}4)cdot P_S=1{,}4P_S$
$begin {cases}
Q_D=100-P_D\
Q_S=P_S\
Q_D=Q_S\
P_D=1{,}4P_S\
end {cases}$
$100-1{,}4P_S=P_S$
$P_S=41{,}(6)$
$P_D=58{,}(3)$
$Q_D=Q_S=41{,}6$
 Пример 2
Пример 2
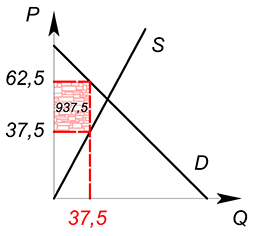
На совершенно конкурентном рынке функция спроса на товар имеет вид $Q_D=100-P_D$, предложения – $Q_S=P_S$, государство вводит стоимостной налог – 40% от цены потребителя. Найти $P_D$, $P_S$, $Q^*$ после введения налога, найти сумму налоговых поступлений.
$P_S=(1-0{,}4)cdot P_D=0{,}6P_D$
Запишем систему:
$begin {cases}
Q_D=100-P_D\
Q_S=P_S\
Q_D=Q_S\
P_S=0{,}6P_D\
end {cases}$
$100-P_D=0{,}6P_D$
$100=1{,}6P_D$
$P_D=62{,}5$
$P_S=37{,}5$
$Q_D=Q_S=37{,}5$
$T=tcdot P_D cdot Q^*$
$T=0{,}4cdot 62{,}5 cdot 37{,}5=937{,}5$
 Пример 3
Пример 3
На рынке работает монополия. $P_D=100-Q_D$, $TC=Q^2 10$, государство ввело налог, равный 40% цены покупки. Найти прибыль фирмы после введения налога
$pi(Q)=0{,}6(100-Q)Q-Q^2-10=60Q-1{,}6Q^2-10$
$pi'(Q)=60-3{,}2Q=0$
$Q=18{,}75$
$pi”(Q)=-3{,}2<0$, максимум
$pi=763{,}4375>0$, фирма остается на рынке
Действие стоимостной субсидии обратно действию налога
Пример 4
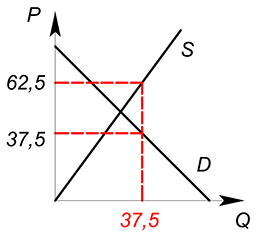
На совершенно конкурентном рынке функция спроса на товар имеет вид $Q_D=100-P_D$, предложения – $Q_S=P_S$, государство вводит стоимостную субсидию – 40% от цены производителя. Найти $P_D$, $P_S$, $Q^*$ после введения налога, найти сумму налоговых поступлений.
$P_D=0{,}6P_S$
$begin {cases}
Q_D=100-P_D\
Q_S=P_S\
Q_D=Q_S\
P_D=0{,}6P_S\
end {cases}$
$100-0{,}6P_S=P_S$
$P_S=62{,}5$
$P_D=37{,}5$
$Q_D=Q_S=37{,}5$
§
§
Возьмем некоторую функцию $y=f(x)$. Возьмем некоторый произвольный $x_1$ из области определения данной функции, ему будет соответствовать единственный $y_1=f(x_1)$. Теперь вместо $x_1$ подставим в имеющуюся функцию $x_2$ (также принадлежащий её области определения). Получим $y_2=f(x_2)$. В зависимости от вида данной функции $y=f(x)$ можем получить, что $y_2=y_1$ или же, что $y_2neq y_1$. Функция реагирует на изменение её аргумента. $y_2$ может отличаться от $y_1$ на большую величину $Delta y$, а может и на маленькую.
Эластичность функции
как раз и показывает степень её реакции а изменение аргумента.
Коэффициент эластичности показывает, на сколько процентов изменяется значение функции при увеличении аргумента на один процент.
$E_x^y=dfrac {Delta F(x) (проценты) }{Delta x (проценты) }=dfrac {Delta y / y }{Delta x / x}=dfrac{Delta y}{Delta x} cdot dfrac{x}{y}$
В данной формуле $x$ традиционно был принят за независимую переменную.
Если нам нужно посчитать эластичность функции в какой-либо точке (когда изменение аргумента стремится к 0), то можно воспользоваться следующей формулой точечной эластичности:
$E=limlimits_{Delta x to 0} dfrac {Delta y}{Delta x} cdot dfrac{x}{y}=y'(x) cdot dfrac{x}{y}$
Пример 1
Функция спроса имеет вид $Q(P)=100-P$, посчитать эластичность в точке $Q=50$.
$Q=50$, значит и $P=50$
$Q'(P)=-1$
$E=-1 cdot dfrac{50}{50}= -1$
Формулой точечной эластичности можно также пользоваться, когда нужно узнать эластичность в окрестностях какой-либо точки – при малых изменениях функции и аргумента (до 10%):
$E=dfrac{Delta y}{Delta x} cdot dfrac{x}{y}=dfrac{y_2-y_1}{x_2-x_1} cdot dfrac{x_1}{y_1}$
Пример 2
При увеличении цены с 50 до 51 д.ед количество покупаемого товара снизилось с 200 до 195 шт. Найти точечную эластичность
$E=dfrac{195-200}{51-50} cdot {50}{200}=-1{,}25$
При больших приращениях функции и аргумента (более 10%) мы ищем чувствительность функции к изменению аргумента на некотором отрезке измерения. Тогда воспользуемся формулой дуговой эластичности, которая поможет избежать проблемы, возникшей бы, если бы мы пользовались формулой для расчета точечной эластичности – при использовании формулы точечной эластичности для подсчета эластичности на отрезке на конечный результат влияет то, какую точку мы считаем $x_1$, а какую $x_2$:
Пример 3
Имеется линейная функция $Q=100-P$, взята точка $A$ c координатами $(25;75)$ и точка $B$ с координатами $(75;25)$ (на первом месте стоит цена). Необходимо посчитать эластичность на отрезке $AB$
Посчитаем по формуле точечной эластичности. Пусть $P_1=x_1=25$, $P_2=x_2=75$. Тогда:
$E=dfrac{25-75}{75-25} cdot dfrac{25}{75}=-dfrac{1}{3}$
Теперь пусть $x_1=75$, $x_2=25$
$E=dfrac{75-25}{25-75} cdot {75}{25}=-3$
Показатели эластичности на отрезке $AB$ различаются в зависимости от того, какую точку $A$ или $B$ принять за начало отрезка. поэтому для расчета эластичности функции при больших изменениях аргумента и зависимой переменной используется формула дуговой эластичности:
$E=dfrac{y_2-y_1}{x_2-x_1} cdot dfrac { dfrac{x_2 x_1}{2}}{dfrac{y_2-y_1}{2}}=dfrac{y_2-y_1}{x_2-x_1} cdot {x_2 x_1}{y_2 y_1}$
В данной формуле для расчета эластичности вторым множителем выступает не координата начальной точки, а координата точки, располагающейся в середине отрезка $AB$. Теперь значение эластичности не зависит от выбора направления движения.
Посчитаем эластичность по новой формуле. $x_1=25$, $x_2=75$
$E=dfrac{25-75}{75-25} cdot dfrac{75 25}{25 75}=-1$
Теперь $x_1=75$, $x_2=25$
$E=dfrac{75-25}{25-75} cdot dfrac{25 75}{75 25}=-1$
Считать эластичность по формуле дуговой эластичности можно и при малых (до 10%) изменениях аргумента и функции. Значение дуговой и точечной эластичности тогда будут близки. Точечная эластичность показывает реакцию функции на изменение аргумента в точке или в её окрестности, дуговая же показывает чувствительность функции к изменению аргумента на некотором отрезке.
Если эластичность функции в какой-любо точке/ на каком-либо отрезке равна 0, то данная функция в этом месте является совершенно неэластичной, если $0< E< 1$, то это неэластичный фрагмент, если $E=1$, то это фрагмент с единичной эластичностью, если $1< E< infty$, то фрагмент функции эластичен, если $E=infty$, то он совершенно эластичен.
§
Пусть у нас имеется фрагмент некоторой функции спроса:
Рассмотрим формулу точечной эластичности:
$E_x^y=y'(x)cdot(dfrac{x}{y})$
В данной записи геометрический смысл первого сомножителя – тангенс угла наклона касательной, проведенной к функции в некоторой интересующей нас точке, второго – тангенс угла наклона луча, проведенного из начала координат к точке, в которой мы хотим вычислить точечную эластичность. Построим:
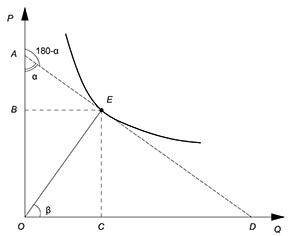
$E_x^y=y'(x)cdot(dfrac{x}{y})=-{tgalpha}cdot{tgbeta}$
$tgalpha=dfrac{BE}{AB}$
$tgbeta=dfrac{CE}{CO}$
$E_x^y=-dfrac{{BE}cdot{CE}}{{AB}cdot{CO}}$
$BE=CO$
$CE=BO$
$E_x^y=-dfrac{BO}{AB}$
Также:
$E_x^y=-dfrac{CD}{CO}$
Аналогично выводится геометрический смысл точечной эластичности предложения, а также любой другой функции (только необходимо следить за тем, какая переменная является зависимой, а какая независимой).
Возьмем функцию предложения:
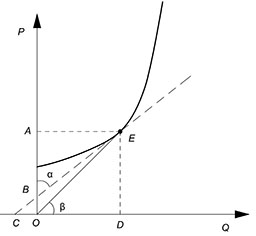
$E_x^y=y'(x)cdot(dfrac{x}{y})={tgalpha}cdot{tgbeta}$
$tgalpha=dfrac{AE}{AB}$
$tgbeta=dfrac{DE}{DO}$
$E_x^y=dfrac{{AE}cdot{DE}}{{AB}cdot{DO}}$
$AE=DO$
$DE=AO$
$E_x^y=dfrac{AO}{AB}$
Также:
$E_x^y=dfrac{CD}{DO}$
Геометрическим смыслом точечной эластичности удобно пользоваться, когда предложена линейная функция.
Пример 1
Дана функция предложения $Q=-10 P$, найти точечную эластичность при $Q=5$
Решим задачу, заодно найдем геометрический смысл точечной эластичности предложения.
$Q=5$, $P=15$
Изобразим нашу функцию, сделаем обозначения:
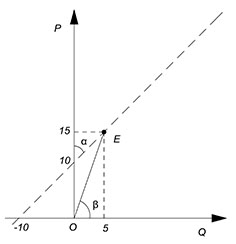
$E_x^y=dfrac{AO}{AB}=dfrac{15}{5}=3$
Геометрический смысл дуговой эластичности:
Рассмотрим случай с функцией спроса:
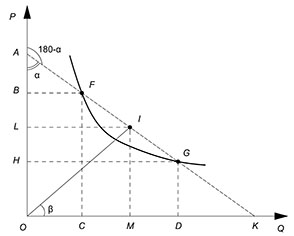
Вычислим дуговую эластичность в точке I.
Помним, что
$E^y_x={dfrac{y_F-y_G}{x_F-x_G}}cdot{dfrac{(x_F x_G)/2}{(y_F y_G)/2}}$
Первый сомножитель – тангенс угла наклона хорды, проведенной через F и G к положительному направлению оси P. Геометрический смысл второго сомножителя – тангенс угла наклона луча, проведенного из начала координат к точке I (I – середина отрезка FG).
$E_x^y=-{tgalpha}cdot{tgbeta}$
$tgalpha=dfrac{IL}{AL}$
$tgbeta=dfrac{IM}{MO}$
$E_x^y=-dfrac{{IL}cdot{AL}}{{IM}cdot{MO}}$
$IL=MO$
$IM=OL$
$E_x^y=-dfrac{LO}{AL}=-dfrac{KM}{MO}$
Пример 2
Пусть имеется некоторая функция спроса. В точке F цена равна 20, а преобретаемое количество товара – 15. В точке G цена равняется 10, покупатели готовы купить по такой цене 30 единиц продукции. Найти дуговую эластичность при переходе из одной точки в другую, используя ее геометрический смысл.
Построим график, проведем хорду через точки F и G, обозначим точку I – середину данного отрезка, проведем луч, выходящий из начала координат к этой точке, сделаем обозначения на осях:
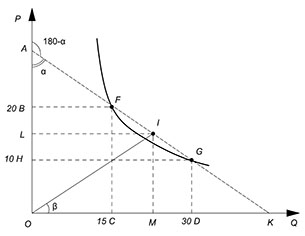
Как мы знаем:
$E_x^y=-dfrac{LO}{AL}=-dfrac{KM}{MO}$
Нам нужны координаты точек L и A. Чтобы узнать координату точки A, выведем функцию хорды:
$ begin{cases}
30=10a b
\
15=20a b
\
end{cases}
$
Получим $Q=45-1,5P$
Откуда координата точки A – $(45;0)$
Координаты точки L – как середины отрезка BH – $dfrac{10 20}{2}=15$ $(15;0)$.
$E_x^y=-dfrac{LO}{AL}=-dfrac{15}{15}=-1$
§
$E={dfrac{Q_{i2}-Q_{i1}}{P_{n2}-P_{n1}}} cdot {dfrac{P_{n1}}{Q_{i1}}}$
$E=Q_{i}'(P_n) cdot {dfrac{P_n}{Q_i}}$
$E={dfrac{Q_{i2}-Q_{i1}}{P_{n2}-P_{n1}}} cdot {dfrac{P_{n2} P_{n1}}{Q_{n2} Q_{i1}}}$
Если перекрестна эластичность больше 0, это указывает на то, что при увеличении цены на другой товар, величина спроса на данный товар растет. Следовательно, товары являются взаимозаменяющими. Если зависимость между ценой другого товара и количеством данного товара отрицательная, то товары являются взаимодополняющими.
§
$E={dfrac{Q_{2}-Q_{1}}{I_{2}-I_{n1}}} cdot {dfrac{I_{1}}{Q_{1}}}$
$E=Q'(I) cdot {dfrac{I}{Q}}$
$E={dfrac{Q_{2}-Q_{1}}{I_{2}-I_{1}}} cdot {dfrac{I_{2} I_{1}}{Q_{2} Q_{1}}}$
Если $E$ принадлежит:
$(-infty;0)$, благо является инфериорным (некачественным)
$(0;infty)$, благо является качественным,
также $(0;1)$ – товар первой необходимости (потребление растет медленнее дохода), 1 – товар с единичной эластичностью, $(1; infty)$ – товар роскоши (потребление растет быстрее дохода)
Эконометрическая модель – это математическая модель
реальной экономической системы (объекта), построенная на статистических данных
Эконометрика синтезирует в себе науки:
экономическую теорию, математическую статистику и экономическую статистику
Проблемой спецификации не является …
расчет оценок параметров эконометрической модели
1. При построении модели множественной регрессии методом пошагового включения переменных на первом этапе рассматривается…
Модель с одной объясняющей переменной, которая имеет с зависимой переменной наибольший коэффициент корреляции
2. В исходное уравнение регрессии 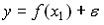 добавляются факторы
добавляются факторы  ,
,  ,
, 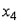
При этом 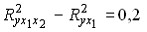 ;
;  ;
;  .
.
Определите, какие дополнительные факторы необходимо
включить в исходное уравнение.
х2 и х3
3. Из двух коллинеарных факторов из модели множественной регрессии исключается тот, для которого абсолютное значение стандартизованного коэффициента …
Меньше
4. Отбор факторов в модель множественной регрессии с использованием метода включения может быть основан на сравнении …
-величины объясненной дисперсии до и после включения =фактора в модель
-величины остаточной дисперсии до и после включения фактора в модель
5. Матрица парных коэффициентов линейной корреляции может служить для решения следующих задач:
-определения тесноты линейной связи между переменными
-выявления мультиколлинеарных факторов
6.
1)Для оценки заработной платы некоторого работника используется следующая модель 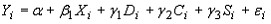 , где
, где 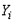 – заработная плата
– заработная плата 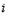 -го работника;
-го работника; 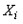 – общий стаж его работы;
– общий стаж его работы;  – переменная, принимающая значение 1, если работник с высшим образованием и 0 в противном случае;
– переменная, принимающая значение 1, если работник с высшим образованием и 0 в противном случае; 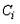 – количество детей у работника;
– количество детей у работника; 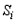 – переменная, принимающая значение 1, если работник мужчина и 0, если женщина. Сколько факторов необходимо представить в модели фиктивными переменными?
– переменная, принимающая значение 1, если работник мужчина и 0, если женщина. Сколько факторов необходимо представить в модели фиктивными переменными?
Ответ: 2
2)Фиктивная переменная может принимать значения:
Ответ: 0, 1
3)В модели необходимо учесть влияние возраста на производительность труда работника. На предприятии работают пенсионеры и лица, не достигшие пенсионного возраста (всего 2 категории). Тогда максимальное количество фиктивных переменных, необходимых для проведения анализа и построения оценок равно…
Ответ: 1
4)В страховой компании решили оценить влияние знака зодиака (всего 12), под которым рожден работник, на производительность его труда. Тогда максимальное количество фиктивных переменных, необходимых для проведения анализа и построения оценок равно…
Ответ: 11
5)Укажите уравнения регрессии, в которых фиктивная переменная D используется только в аддитивной форме:
Ответ: Y=b0 b1X2 b2D, Y=b0 b1X b2D
6)Для оценки заработной платы некоторого работника используется следующая модель 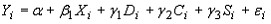 , где
, где 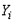 – заработная плата
– заработная плата 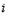 -го работника;
-го работника; 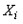 – общий стаж его работы;
– общий стаж его работы;  – переменная, принимающая значение 1, если работник с высшим образованием и 0 в противном случае;
– переменная, принимающая значение 1, если работник с высшим образованием и 0 в противном случае; 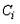 – переменная, принимающая значение 1, если у работника есть дети и 0, если нет,
– переменная, принимающая значение 1, если у работника есть дети и 0, если нет, 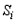 – переменная, принимающая значение 1, если работник мужчина и 0, если женщина. Сколько факторов необходимо представить в модели фиктивными переменными?
– переменная, принимающая значение 1, если работник мужчина и 0, если женщина. Сколько факторов необходимо представить в модели фиктивными переменными?
Ответ: 3
7)В модели необходимо учесть влияние уровня образования на заработную плату работника. На предприятии работают люди со средним специальным, высшим и незаконченным высшим образованием (всего 3 категории). Тогда максимальное количество фиктивных переменных, необходимых для проведения анализа и построения оценок равно…
Ответ: 2
8)Проводится эконометрическое моделирование зависимости объема продаж компании от ряда факторов: х1 – цены на товар, х2 – степени известности торговой марки фирмы, х3 – дохода потребителя, х4 – уровня интенсивности рекламной деятельности (высокий уровень – массированная реклама; средний уровень – регулярно повторяющаяся; низкий уровень – время от времени повторяющаяся). Фиктивными переменными в модели не являются …
Ответ: х1, х3
9)Исследуется зависимость потребления кофе от ряда факторов: х1 – марки кофе, х2 – уровня крепости кофе (крепкий, средней крепости, слабой крепости), х3 – дохода потребителя, х4 – цены на кофе. Фиктивными переменными в модели не являются …
Ответ: х3, х4
10)Фиктивными переменными в уравнении множественной регрессии могут быть …
Ответ: качественные переменные, преобразованные в количественные; переменные, исходные значения которых не имеют количественного значения
§
На рисунке отражены результаты теста Дарбина-Уотсона. 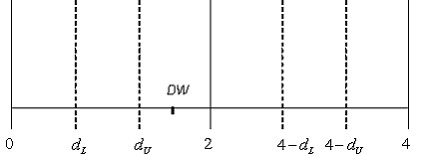 Где
Где 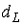 ,
, 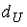 – соответственно нижняя и верхняя границы для критического значения, а
– соответственно нижняя и верхняя границы для критического значения, а 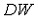 – наблюдаемое значения критерия Дарбина-Уотсона (
– наблюдаемое значения критерия Дарбина-Уотсона ( 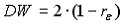 , где
, где 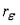 – коэффициент автокорреляции остатков). Можно сделать вывод что…
– коэффициент автокорреляции остатков). Можно сделать вывод что…
в остатках регрессионной модели присутствует отрицательная автокорреляция.
в остатках регрессионной модели присутствует положительная автокорреляция.
нет оснований отвергнуть нулевую гипотезу об отсутствии автокорреляции в остатках регрессионной модели (автокорреляция в остатках отсутствует).
нельзя ни отклонить, ни принять нулевую гипотезу об отсутствии автокорреляции в остатках регрессионной модели (зона неопределенности).
Требования независимости регрессионных остатков и объясняющих переменных в классической линейной регрессионной модели  обуславливает получение ______ оценок параметров регрессии.
обуславливает получение ______ оценок параметров регрессии.
состоятельных
смещенных
эффективных
несмещенных
Тест Дарбина-Уотсона применяется для выявления в регрессионной модели _______ остатков.
автокорреляции
гетероскедастичности
гомоскедастичности
порядка автокорреляции
Верным утверждением является …
проблема гетероскедастичности не характерна для перекрестных данных
остатки характеризуется постоянной дисперсией в случае гетероскедастичности
наличие гетероскедастичности невозможно выявить, пользуясь критерием Дарбина-Уотсона
статистические выводы на основе критерия Фишера при гетероскедастичности являются надежными
Тест Спирмена, используемый для обнаружения гетероскедастичности остатков, основан на …
предположении пропорциональности между дисперсией остатков и независимой переменной с коэффициентом 
сравнении рангов значений зависимой переменной  и остатков модели
и остатков модели 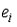
минимизации остатков 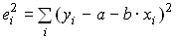
сравнении рангов значений независимой переменной 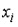 и остатков модели
и остатков модели 
График зависимости остатков et от времени t свидетельствует о наличии… 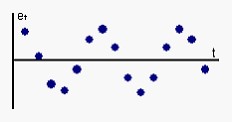
нелинейной связи между объясняющими переменными
отсутствии корреляции в остатках
автокорреляции остатков
мультиколлинеарности данных
Дана последовательность операций:1. оценка параметров регрессии2. вычисление регрессионных остатков3. вычисление статистики Дарбина-Уотсона4. определение верхнего и нижнего значения распределения Дарбина-Уотсона Приведенный алгоритм предназначен для диагностики наличия …
мультиколлинеарности
автокорреляции остатков
гетероскедастичности
гомоскедастичности
Отсутствие систематического смещения случайного возмущения 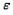 в регрессионной модели
в регрессионной модели  представляет собой …
представляет собой …
условие статистической значимости регрессионного уравнения
одну из основных предпосылок метода наименьших квадратов для оценки параметров регрессии
теорему Гаусса-Маркова
условие нормального распределения фактора 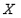
Отрицательная автокорреляция остатков имеет место, когда…
знаки соседних отклонений, как правило, противоположны
подавляющее большинство отклонений отрицательно
сумма всех отклонений отрицательна
знаки соседних отклонений, как правило, одинаковые
Отсутствие автокорреляции в остатках предполагает, что значения ______ модели не зависят друг от друга.
результативной переменной
остатков
параметров
факторной переменной
7 вариант(Свойства оценок параметров эконометрической модели, получаемых при помощи МНК.)
1. Укажите условия, которые выполняются, если оценки параметров уравнения регрессии обладают свойствами состоятельности, эффективности и несмещенности. равенство нулю математического ожидания остатков; наименьшая дисперсия остатков
2. Если предпосылки метода наименьших квадратов не выполняются, то оценки параметров уравнения регрессии могут не обладать свойствами …Эффективности и несмещённости
3. Если оценки параметров уравнения регрессии обладают свойствами состоятельности, эффективности и несмещенности, то …при большом числе выборочных оцениваний остатки не будут накапливаться; возможен переход от точечного оценивания к интервальному
4. Если оценки параметров линейного уравнения регрессии обладают свойством несмещенности, то математическое ожидание остатков …
Равно 0
5. Минимальная дисперсия остатков характерна для оценок, обладающих свойством …эффективности
6. Переход от точечного оценивания к интервальному возможен, если оценки являются эффективными и несмещенными
7. Несмещенная оценка  параметра
параметра 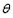 имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра
имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра 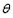 , вычисленных по выборкам одного и того же объема
, вычисленных по выборкам одного и того же объема 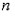 . Такая оценка называется … эффективной
. Такая оценка называется … эффективной
8. Если оценка параметра эффективна, то это означает …наименьшую дисперсию остатков; возможность перехода от точечного оценивания к интервальному
9. Если оценки параметров линейного уравнения регрессии обладают свойством эффективности, то дисперсия остатков характеризуется …минимальной величиной
10. Если оценки параметров уравнения регрессии, полученных при помощи метода наименьших квадратов обладают свойствами несмещенности, эффективности и состоятельности, то …
возможен переход от точечного оценивания к интервальному; математическое ожидание остатков равно нулю и они характеризуются минимальной дисперсией
Вариант 8. ОМНК.
1.Случайные составляющие регрессионной модели не имеют постоянной дисперсии или коррелированны между собой. Тогда автоковариационная матрица случайных составляющих имеет вид …
Ответ:
2. Для преодоления проблемы автокорреляции служит …
Ответ: обобщенный метод наименьших квадратов
§
ü 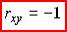
ü 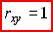
10. Если значение коэффициента корреляции, рассчитанное для линейного уравнения регрессии 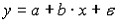 равно единице, то …
равно единице, то …
ü связь между переменными у и х функциональная
ü величина  оказывает существенное влияние на переменную у
оказывает существенное влияние на переменную у
11. Пусть  и
и 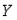 — случайные величины,
— случайные величины,  — эмпирическое корреляционное отношение. Свойствами эмпирического корреляционного отношения являются:
— эмпирическое корреляционное отношение. Свойствами эмпирического корреляционного отношения являются:
ü если  , то между переменными корреляционная связь отсутствует
, то между переменными корреляционная связь отсутствует
ü корреляционное отношение есть неотрицательная величина, не превосходящая единицы: 
№10. Оценка качества подбора уравнения.
1. 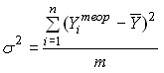 где m– число факторных признаков. Приведена формула подсчета
где m– число факторных признаков. Приведена формула подсчета
Укажите ответ:
ü объясненной дисперсии
__2_Значение коэффициента детерминации составило 0,81, следовательно уравнением регрессии объяснено _____ дисперсии зависимой переменной.
ü 81 %
3. Рассматривается регрессионная модель 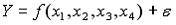 , где – линейная функция. Количество наблюдений
, где – линейная функция. Количество наблюдений  =25. Остаточная сумма квадратов равна 440. Тогда остаточная дисперсия на одну степень свободы равна …
=25. Остаточная сумма квадратов равна 440. Тогда остаточная дисперсия на одну степень свободы равна …
ü 
4. Случайными воздействиями обусловлено 12% дисперсии результативного признака, следовательно, значение коэффициента детерминации составило …
ü 0,88
5. Коэффициент детерминации …?
ü является безразмерной величиной
6. Значение коэффициента детерминации составило 0,9, следовательно …
ü уравнением регрессии объяснено 90% дисперсии результативного признака y
7. Пусть 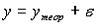 , где y – фактическое значение зависимой переменной,
, где y – фактическое значение зависимой переменной, 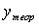 – теоретическое , рассчитанное по уравнению значение зависимой переменной (объясненное уравнением регрессии),
– теоретическое , рассчитанное по уравнению значение зависимой переменной (объясненное уравнением регрессии), 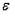 – ошибка модели. Тогда значение
– ошибка модели. Тогда значение  характеризует дисперсию …
характеризует дисперсию …
ü фактических значений зависимой переменной
8. 
ü 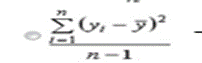
9.

ü 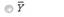
10. Для множественной линейной регрессии с числом факторов вычисляют коэффициент детерминации с учетом величины дисперсии на одну степень свободы. В этом случае скорректированный коэффициент детерминации находят по формуле …
ü 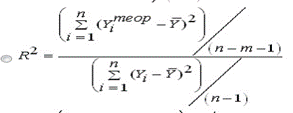
Вариант 11.
№1
Вопрос: В таблице представлены результаты дисперсионного анализа. Значение общей суммы квадратов можно определить, как … 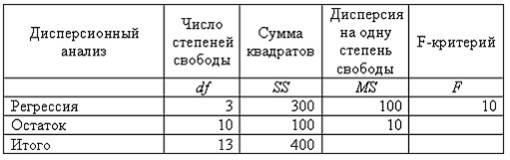
Ответ: -число на пересечении строки “Итого” и столбца “SS”
-сумму чисел, определенных на пересечении столбца “SS” и строк “Регрессия” и “Остаток”
№2
Вопрос: В таблице представлены результаты дисперсионного анализа. Значение остаточной дисперсии на одну степень свободы можно определить, как …
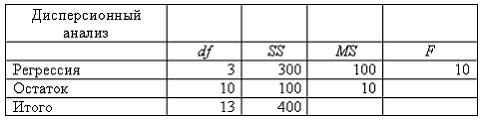
Ответ: -отношение чисел, определенных на пересечении строки “Остаток” и столбцов “SS” и “df”
-число на пересечении строки “Остаток” и столбца “MS”
№3
Вопрос: Если расчетное значение F–критерия Фишера меньше табличного, то можно сделать вывод о …
Ответ: -незначимости (несущественности) моделируемой зависимости
-статистической незначимости построенной модели
№4
Вопрос: В таблице представлены результаты дисперсионного анализа. Значение объясненной (факторной) суммы квадратов можно определить, как …
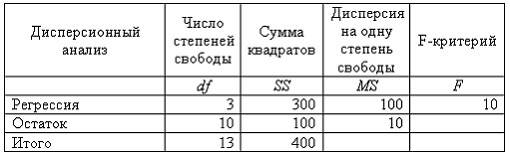
Ответ: -число на пересечении строки “Регрессия” и столбца “SS”
-разность чисел, определенных на пересечении столбца “SS” и строк “Итого” и “Остаток”
№5
Вопрос: В таблице представлены результаты дисперсионного анализа. Значение остаточной суммы квадратов можно определить, как …

Ответ: – разность чисел, определенных на пересечении столбца “SS” и строк “Итого” и “Регрессия”
-число на пересечении строки “Остаток” и столбца “SS”
№6
Вопрос: Какие статистические гипотезы выдвигаются при проверке статистической значимости построенной модели?
Ответ: – нулевая о статистической незначимости
– альтернативная о статистической значимости
№7
Вопрос: В таблице представлены результаты дисперсионного анализа. Расчетное значение F-критерия можно определить, как …
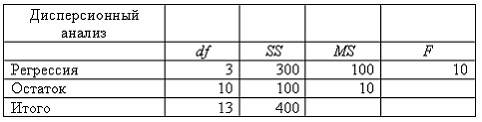
Ответ: – отношение чисел, определенных на пересечении столбца “MS” и строк “Регрессия” и “Остаток”
– число на пересечении строки “Регрессия” и столбца “F”
№8
Вопрос: При проверке статистической значимости построенной модели проводят сравнение …
Ответ: – табличного значения критерия Фишера
-расчетного значения критерия Фишера
№9
Вопрос: Статистические гипотезы используются для оценки статистической значимости …
Ответ: – уравнения
-оцениваемых параметров
№10
Вопрос: В таблице представлены результаты дисперсионного анализа. Значение объясненной (факторной) дисперсии на одну степень свободы можно определить, как …
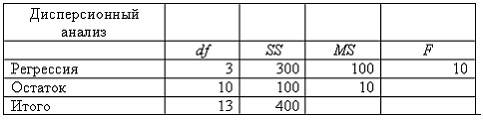
Ответ: – число на пересечении строки “Регрессия” и столбца “MS”
-отношение чисел, определенных на пересечении строки “Регрессия” и столбцов “SS” и “df”
ТЕСТ 12
1.Если коэффициент регрессии является несущественным, то для него выполняются условия …
· доверительный интервал проходит через ноль
· расчетное значение t–критерия Стьюдента по модулю меньше табличного
2. Если доверительный интервал для коэффициента регрессии содержит 0, то справедливы следующие утверждения:
· коэффициент регрессии статистически незначим
· фактическое значение статистики Стьюдента для этого коэффициента по модулю меньше критического (табличного)
Выберите пропущенное в таблице
значение 
· 12
4.Коэффициент регрессии считается статистически значимым, если справедливы следующие утверждения:
· доверительный интервал для этого коэффициента не содержит 0
· фактическое значение статистики Стьюдента для этого коэффициента по модулю больше критического (табличного)
5. Критическое значение критерия Стьюдента определяет минимально возможную величину, допускающую принятие гипотезы о …
· статистической значимости (существенности) параметра
6. Если 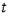 -критерий, вычисленный для оценки параметра регрессии меньше значения
-критерий, вычисленный для оценки параметра регрессии меньше значения 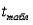 , вычисленного по таблицам распределения Стьюдента, то на данном уровне значимости …
, вычисленного по таблицам распределения Стьюдента, то на данном уровне значимости …
· не отвергается гипотеза о равенстве нулю параметра для генеральной совокупности
7. С помощью частного 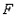 -критерия можно проверить значимость
-критерия можно проверить значимость  -го коэффициента чистой регрессии в предположении, что
-го коэффициента чистой регрессии в предположении, что  -й фактор в уравнение множественной регрессии …
-й фактор в уравнение множественной регрессии …
· был включен последним
§
· его значение признается отличным от нуля
9. Пусть t – рассчитанная для коэффициента регрессии статистика Стьюдента, а t крит – критическое значение этой статистики. Коэффициент регрессии считается статистически значимым, если выполняются следующие неравенства:
· t крит
· t > t крит
10. Для парной линейной регрессии y=a bx e проверка гипотезы о значимости коэффициента регрессии b равносильна проверкам гипотез о значимости:
· коэффициента детерминации
· линейной связи между x и y
Прошу прощения за не все решенные ответы.
1.Зависимость 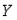 от
от 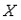 , задаваемая функцией вида
, задаваемая функцией вида 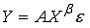 (
(  ), является возрастающей функцией …
), является возрастающей функцией …
При 0<b<1
2. Функции Торнквиста относятся к классу _________ моделей.
Обратной
3. Зависимость объема производства 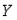 от использования ресурса
от использования ресурса 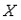 , задаваемая функцией вида
, задаваемая функцией вида 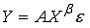 (
(  ,
, 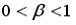 ) является …
) является …
Возрастающей функцией
Выпуклая вверх
4. При выборе спецификации нелинейная регрессия используется, если …
между экономическими показателями обнаруживается нелинейная зависимость
5. Нелинейную модель зависимостей экономических показателей нельзя привести к линейному виду, если …
нелинейная модель является внутренне нелинейной
6. Производственная функция Кобба-Дугласа относится к классу _________ моделей.
степенных
7. Зависимости 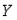 от
от  , задаваемая функцией вида
, задаваемая функцией вида  (
( 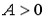 ), является выпуклой вниз функцией …
), является выпуклой вниз функцией …
При b<0
При 0<b<1
8. Зависимость спроса на товары первой необходимости от дохода (функция Торнквиста, 
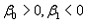 ) характеризуется обратной эконометрической моделью с начальным уровнем
) характеризуется обратной эконометрической моделью с начальным уровнем 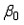 вида …
вида …
9.

10. Зависимость спроса 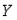 на благо от его цены
на благо от его цены 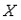 , задаваемая функцией вида
, задаваемая функцией вида 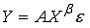 (
( 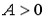 ,
, 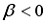 ) является …
) является …
Убывающая функция
Выпуклая вниз
| 1Вопрос: | Все нижеприведенные нелинейные модели можно свести к модели множественной линейной регрессии W = b0 b1·U b2·V. Установите соответствие между видом нелинейной модели и соотношениями между исходными переменными Y, X, Z и новыми переменными W, U, V линеаризованной модели. |
| Соотнесите: | |
| 2Вопрос: | Включение случайного отклонения мультипликативным способом позволяет линеаризовать регрессионную модель вида … |
| Укажите ответ: |  |
| Вопрос: | 3Установите соответствие между видом модели и ее характеристиками. |
| Соотнесите: | |
| Вопрос: | 4Эконометрической моделью, приводимой к линейной регрессионной модели при логарифмировании и соответствующей подстановке, является … |
| Укажите ответ: | 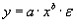 |
| Вопрос: | 5Эконометрическую модель, линейную по параметрам и нелинейную по переменным с аддитивным включением случайного возмущения … |
| Укажите ответ: | всегда можно свести к классической регрессионной модели с помощью соответствующей подстановки |
| 6Вопрос: | Эконометрическая модель 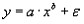 является… является… |
| Укажите ответ: | нелинейной по параметрам и нелинейной по переменным |
| 7Вопрос: | Замена 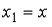 ; ; 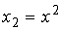 подходит для уравнения … подходит для уравнения … |
| Укажите ответ: |  |
| 8Вопрос: | Все нижеприведенные нелинейные модели можно свести к модели множественной линейной регрессии W = b0 b1·U b2·V. Установите соответствие между видом нелинейной модели и соотношениями между исходными переменными Y, X, Z и новыми переменными W, U, V линеаризованной модели. |
| Соотнесите: | |
| Вопрос: | 9Все нижеприведенные нелинейные модели можно свести к модели множественной линейной регрессии W = b0 b1·U b2·V. Установите соответствие между видом нелинейной модели и соотношениями между исходными параметрами a, b, c и параметрами b0 , b1, b2 линеаризованной модели. |
| Соотнесите: | |
| Вопрос: | 10Все нижеприведенные нелинейные модели можно свести к модели множественной линейной регрессии W = b0 b1·U b2·V. Установите соответствие между видом нелинейной модели и соотношениями между исходными параметрами a, b, c и параметрами b0 , b1, b2 линеаризованной модели. |
| Соотнесите: |
16 тест
1) Гипотеза о значимости в целом уравнения нелинейной регрессии проверяется с помощью критерия…
Фишера
2)
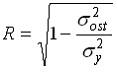
3) Индекс корреляции для нелинейных форм связи находят по формуле …

4) Нелинейная связь между рассматриваемыми признаками тем теснее, чем значение индекса корреляции ближе к …
5) Значение индекса корреляции находится в пределах …
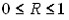
6) Квадрат индекса корреляции для нелинейных форм называется …
индексом детерминации
7) Коэффициент детерминации для нелинейной модели часто называют…
индексом детерминации
8) Выражение 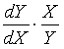 позволяет вычислить значение …
позволяет вычислить значение …
коэффициента эластичности
9) Значение индекса детерминации, рассчитанное для нелинейного уравнения регрессии характеризует долю дисперсии результативного признака, _____, в общей дисперсии результативного признака.
объясненную нелинейной регрессией
10) Для степенной функции 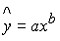 формула для определения
формула для определения 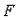 –критерия
–критерия 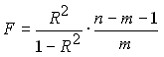 примет вид …
примет вид …
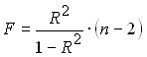
17 вариант(Временные ряды данных: характеристики и общие понятия.)
1.Временным рядом является совокупность значений …
последовательных моментов (периодов) времени и соответствующих им значений экономического показателя; экономического показателя для однотипных объектов на определенный момент времени
2.Временной ряд содержит сезонную компоненту, если на его уровни оказывают влияние факторы только _____ характера
Сезонного
3. Временной ряд характеризует …данные, описывающие один объект за ряд последовательных моментов (периодов) времени
4. Временным рядом является …
значения временных характеристик и соответствующие им значения экономического показателя; совокупность значений экономического показателя за несколько последовательных моментов (периодов времени)
5. Факторы, формирующие общую (в длительной перспективе) тенденцию в изменении анализируемого признака, называются …
Долговременными
6. Если временной ряд представлен в виде произведения соответствующих компонент, то полученная модель носит название …мультипликативной
7. Факторы, описывающие сезонную компоненту временного ряда, могут характеризоваться _____ воздействием на экономический показатель.
сезонным; периодическим
8. Среди факторов, оказывающих влияние на уровень временного ряда можно назвать …сезонные колебания и тенденцию; тенденцию и случайные факторы
9. Модели, построенные на основе данных, характеризующих поведение исследуемого объекта за ряд последовательных моментов времени, называются…моделями временных рядов
10. Уровнем временного ряда является значение …
экономического показателя в данный момент (период времени); заданного момента (периода) времени и соответствующее ему значение экономического показателя
Значение коэффициента автокорреляции второго порядка характеризует связь между …
двумя временными рядами
исходными уровнями и уровнями второго временного ряда
исходными уровнями и уровнями этого же ряда, сдвинутыми на 2 момента времени
исходными уровнями и уровнями другого ряда, сдвинутыми на 2 момента времени
При выявлении структуры временного ряда проводят анализ …
существенности параметров
графика зависимости значений уровня ряда от времени
автокорреляционной функции
матрицы парных коэффициентов линейной корреляции
Для обнаружения автокорреляции первого порядка используется критерий …
Чоу
Дарбина-Уотсона
Фишера
Стьюдента
С помощью автокорреляционной функции и коррелограммы можно выявить …
величину коэффициента детерминации
структуру временного ряда
тип регрессионной зависимости
оптимальную величину лага
Данная коррелограмма 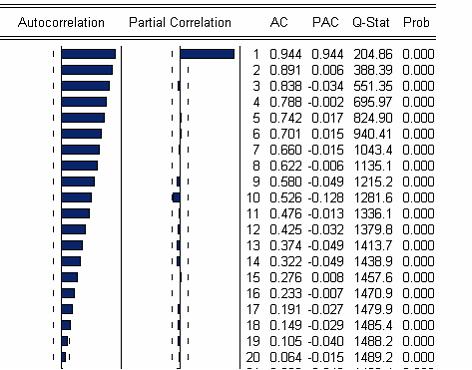 соответствует процессу …
соответствует процессу …
белого шума
авторегресси первого порядка AR(1)
скользящего среднего первого порядка МА(1)
смешанного процесса аворегрессии и скользящего среднего ARMA(1,1)
Коррелограммой временного ряда 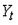 называют график …
называют график …
зависимости уровней ряда переменной 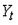 от времени t
от времени t
значений автокорреляционной функции данного ряда
трендовой компоненты временного ряда 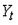
график сезонной составляющей временного ряда
На основе анализа временного ряда построена следующая таблица  Период сезонных колебаний равен
Период сезонных колебаний равен
8
9
2
4
Коэффициент автокорреляции уровней временного ряда характеризует …
качество построенной модели временного ряда
значение коэффициента корреляции между двумя рядами, первый из которых является исходным, а второй получен путем сдвига исходного ряда на заданное число уровней
тесноту линейной связи между уровнями исходного временного ряда и уровнями этого же ряда, сдвинутыми на несколько моментов (периодов)
тесноту связи между уровнями временного ряда и значениями моментов (периодов) времени
Высокое значение коэффициента автокорреляции порядка  для уровней временного ряда свидетельствует о том, что исследуемый ряд содержит (помимо тенденции) …
для уровней временного ряда свидетельствует о том, что исследуемый ряд содержит (помимо тенденции) …
разладочную случайную компоненту
ярко выраженный тренд
только случайную компоненту
колебания с периодом 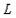
1.Пусть 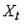 – значения временного ряда с квартальными наблюдениями,
– значения временного ряда с квартальными наблюдениями, 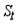 – аддитивная сезонная компонента, причем для первого квартала года
– аддитивная сезонная компонента, причем для первого квартала года 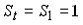 , для второго квартала года
, для второго квартала года 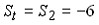 , для третьего квартала года
, для третьего квартала года 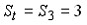 . Определите оценку сезонной компоненты для четвертого квартала года
. Определите оценку сезонной компоненты для четвертого квартала года 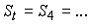
2.Методами аналитического выравнивания уровней временного ряда могут служить:
– метод скользящей средней
– построение уравнения регрессии, характеризующего зависимость уровней ряда от времени
3.Факторами, оказывающими влияние на уровень временного ряда являются факторы …
– формирующие тенденцию и сезонные колебания
– формирующие сезонные колебания и случайные воздействия
4. Для аддитивной модели временного ряда: Yt – уровень временного ряда, T – тренд, S – сезонные колебания, E – случайная величина. Тогда для модели справедливо выражение …
T = Yt – (S E)
T E = Yt – S
5. Пусть 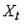 – значения временного ряда с квартальными наблюдениями,
– значения временного ряда с квартальными наблюдениями, 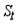 –мультипликативная сезонная компонента, причем для первого квартала года
–мультипликативная сезонная компонента, причем для первого квартала года  , для второго квартала года
, для второго квартала года  , для четвертого квартала года
, для четвертого квартала года 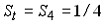 . Определите оценку сезонной компоненты для третьего квартала года
. Определите оценку сезонной компоненты для третьего квартала года 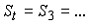
6. Пусть уровень временного ряда Yt формируется под влияние каких– либо из компонент: тренд (T), сезонные колебания (S) и случайные факторы (Е). Тогда аддитивная модель временного ряда может быть представлена в виде …
Y t = Т S E
Y t = T E
7. Пусть 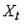 – значения временного ряда с квартальными наблюдениями,
– значения временного ряда с квартальными наблюдениями, 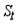 –мультипликативная сезонная компонента, причем для первого квартала года
–мультипликативная сезонная компонента, причем для первого квартала года 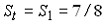 , для третьего квартала года
, для третьего квартала года 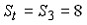 , для четвертого квартала года
, для четвертого квартала года 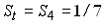 . Определите оценку сезонной компоненты для второго квартала года
. Определите оценку сезонной компоненты для второго квартала года 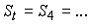
8. Пусть 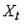 – значения временного ряда с квартальными наблюдениями,
– значения временного ряда с квартальными наблюдениями, 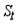 – аддитивная сезонная компонента, причем для второго квартала года
– аддитивная сезонная компонента, причем для второго квартала года  , для третьего квартала года
, для третьего квартала года 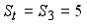 , для четвертого квартала года
, для четвертого квартала года 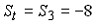 . Определите оценку сезонной компоненты для первого квартала года
. Определите оценку сезонной компоненты для первого квартала года 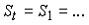
9.Пусть  – значения временного ряда с квартальными наблюдениями,
– значения временного ряда с квартальными наблюдениями,  – мультипликативная сезонная компонента, причем для первого квартала года
– мультипликативная сезонная компонента, причем для первого квартала года  , для второго квартала года
, для второго квартала года 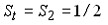 , для четвертого квартала года
, для четвертого квартала года 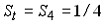 . Определите оценку сезонной компоненты для третьего квартала года
. Определите оценку сезонной компоненты для третьего квартала года 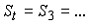
10. Аддитивная модель временных рядов не применяется в случаях:
– когда амплитуда сезонных (циклических) колебаний уменьшается
– когда амплитуда сезонных (циклических) колебаний увеличивается
20 вариант
стационарного стохастического процесса.
9. На рисунке  представлена реализация процесса, нестационарного по математическому ожиданию и периодически нестационарного по дисперсии
представлена реализация процесса, нестационарного по математическому ожиданию и периодически нестационарного по дисперсии
10. Белым шумом” называется чисто случайный процесс
В поведенческих уравнениях структурной формы системы взаимосвязанных уравнений параметры неизвестны и подлежат оценке
| Укажите преимущества использования системы эконометрических уравнений перед изолированными уравнениями регрессии: система уравнений моделирует реальную взаимосвязь на более высоком уровне, чем изолированное уравнение регрессии учитывается взаимозависимость переменных |
Система эконометрических уравнений включает в себя следующие переменные:
предопределенные
зависимые
Укажите справедливые утверждения по поводу системы эконометрических уравнений:
включает множество эндогенных и множество экзогенных переменных
система уравнений, каждое из которых может содержать эндогенные переменные других уравнений
Граф взаимосвязи различных переменных в системе эконометрических уравнений имеет вид: Лаговые переменные Эндогенные переменные Экзогенные переменные 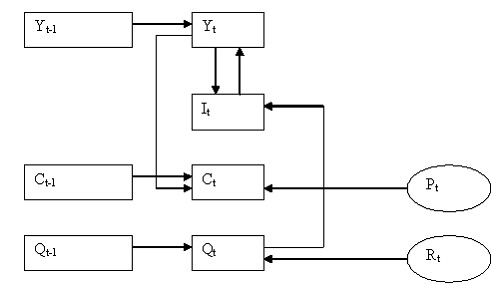 Тогда соответствующая система эконометрических уравнений запишется …
Тогда соответствующая система эконометрических уравнений запишется …
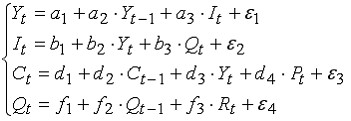
Система одновременных уравнений — это система, в которой
одни и те же эндогенные переменные  входят в левую часть одних уравнений и в правую часть других уравнений
входят в левую часть одних уравнений и в правую часть других уравнений
В систему одновременных уравнений входят регрессионные уравнения, содержащие случайную составляющую и параметры, которые требуется оценить. В качестве независимых переменных эти уравнения могут включать не только факторные, но и результативные признаки из других уравнений системы. Эти регрессионные уравнения называются
поведенческими
§
1. Система уравнений считается неидентифицируемой, если …
ü -хотя бы одно уравнение системы является неидентифицируемым
2. Уравнение системы считается идентифицируемым в соответствии с достаточным условием идентифицируемости, если …
ü число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, равно числу эндогенных переменных в данном уравнении без одной
Для указанной схемы взаимосвязей между переменными
справедливы утверждения:
ü может быть описана с помощью системы рекурсивных уравнений
ü включает 3 уравнения
Для указанной схемы взаимосвязей между переменными
справедливы утверждения:
ü включает 2 уравнения
ü может быть описана с помощью системы одновременных уравнений
5. Для оценки параметров структурной модели системы необходимо …
ü чтобы все уравнения системы были идентифицируемы или сверхидентифицируемы
Укажите существующие классы эконометрических систем: ?
Выберите несколько ответов:
система одновременных уравнений
система независимых уравнений
система нормальных уравнений
система стандартных уравнений
Для указанной схемы взаимосвязей между переменными
справедливы утверждения:
ü может быть описана с помощью системы одновременных уравнений
ü включает 2 уравнения
Для указанной схемы взаимосвязей между переменными

справедливы утверждения:
ü включает 3 уравнения
ü может быть описана с помощью системы независимых уравнений
24 вариант
1. Метод, суть которого состоит в использовании в качестве инструментальной переменной теоретической оценки переопределенной переменной, полученной на базе экзогенных (или предопределенных) переменных модели, является методом наименьших квадратов.
Двушаговым
2. Для сверхидентифицируемой структурной формы системы одновременных уравнений при оценке параметров применяется ______ метод наименьших квадратов.
Двухшаговый
3. Косвенный метод наименьших квадратов применим для …
Идентифицируемой системы одновременных уравнений
4. Оценки параметров идентифицируемой системы эконометрических уравнений могут быть найдены с помощью ______ метода наименьших квадратов.
Косвенного
5. Оценки параметров сверхидентифицируемой системы эконометрических уравнений могут быть найдены с помощью …
Двушагового МНК
6. Приведена последовательность операций: 1. заданная система одновременных уравнений из структурной формы преобразуется в приведенную форму 2. оценки параметров приведенной формы находятся традиционным методом наименьших квадратов 3. по оценкам параметров приведенной формы вычисляются оценки структурных параметров.Этот алгоритм соответствует _____ методу наименьших квадратов.
Косвенному
7. Двухшаговый метод наименьших квадратов является частным случаем …
Метода инструментальных переменных
8. Приведена последовательность операций:1. заданная система одновременных уравнений из структурной формы преобразуется в приведенную форму2. оценки параметров приведенной формы находятся традиционным методом наименьших квадратов3. определение расчетных значений эндогенных переменных, которые выступают в качестве факторов в структурной форме модели4. определение структурных параметров каждого уравнения в отдельности традиционным методом наименьших квадратов, используя в качестве факторов входящие в это уравнение предопределенные переменные и расчетные значения эндогенных переменных, полученные на первом шаге.Этот алгоритм соответствует ____ методу наименьших квадратов.
Двухшаговому
9. Приведена последовательность операций:1. к системе одновременных уравнений применяется обобщенный метод наименьших квадратов с целью устранения корреляции случайных отклонений2. заданная система одновременных уравнений из структурной формы преобразуется в приведенную форму3. оценки параметров приведенной формы находятся традиционным методом наименьших квадратов4. определение расчетных значений эндогенных переменных, которые выступают в качестве факторов в структурной форме модели5. определение структурных параметров каждого уравнения в отдельности традиционным методом наименьших квадратов, используя в качестве факторов входящие в это уравнение предопределенные переменные и расчетные значения эндогенных переменных, полученные на первом шаге.Этот алгоритм соответствует _____ методу наименьших квадратов.
Трехшаговому
10. Неидентифицируемую модель в виде системы одновременных уравнений можно превратить в точно идентифицируемую …






